Arrays and pointers
In Java there is just one way to make an array:
int A[] = new int[100];
C++, on the other hand, offers two different ways to make an array.
The first method is to make an automatic array:
int A[100]; // A is an array of 100 ints
This is called an automatic array because it is designed to vanish automatically when you leave the scope where you created it. For example, if you set up an automatic array as a local variable in a function or method, the array will disappear automatically as soon as you exit that function.
The second method uses a combination of a pointer variable and the new operator.
int *A = new int[100]; // A points to an array of 100 ints
Whether you create the array using method 1 or method 2, you interact with the array in the same way that you would in a Java program. You use the array index notation to access and work with individual cells in the array.
for(int n = 0;n < 100;n++) A[n] = (n+1)*(n+1); // Fill the array with a list of squares int total = 0; for(int n = 0;n < 100;n++) total += A[n]; // Add up the squares
If you created the array using method 1 above, the array will vanish automatically when you exit the scope where it was created. If you created the array via the new operation, you will need to explictly make the array go away when you are done with it by using the delete[] operator:
delete[] A;
As an alternative to using the traditional array index notation, you can also use a pointer to access and interact with the elements in an array.
The process begins by making a copy of the pointer that points to the array:
int *ptr = A; // ptr now also points to the start of the array.
This pointer points to the first element in the array. You can dereference that pointer to access the array element.
*ptr = 12; // ptr points to the first location in the array. // This will set the first location in the array to 12. int y = *ptr; // Copy the value that ptr points to into y
Pointer variables that point into an array can also be moved around in the array via the pointer increment and decrement operations.
ptr++; // ptr now points to the second data item in the array ptr--; // ptr now points to the first data item in the array
Pointer variables that point into an array can also be modified via pointer arithmetic.
int *end = A + 100; // end points 100 spaces past the start // of A, which is just beyond the end of the array
Finally, pointer variables can be compared via the usual == and != comparison operators. Here is some code that uses a pointer to initialize the contents of an array. Note the use of the != comparison operator in the loop.
int *A = new int[100];
int *ptr = A;
int *end = A + 100;
while(ptr != end) {
*ptr = 0;
ptr++;
}
A sorting task
These lecture notes are going to take us through two iterations of a program that performs a simple task. We are going to write a program that can read a list of integers from a text file, sort those integers with an elementary sorting algorithm, and then write the sorted list to a second text file. In the first iteration we will write the program using conventional array notation. In the second iteration we will accomplish the same task working solely with pointers.
To read a list of integers from a text file using an ifstream, we will use the following code.
std::ifstream in; // Declare the ifstream object
in.open("numbers.txt"); // Open the file
int x;
while(in >> x) { // Read a number from the file
// Do something with x
}
in.close(); // Close the file
If you are using Visual Studio, this code will work as is, as long as you make sure the text file named numbers.txt is located in the same directory as the source code for your program. On Xcode, you will have to replace the file name in the open function with the full path to the file in question.
This example demonstrates the "read until done" paradigm with an ifstream. The statement in >> x reads a single int from the ifstream each time we execute it. As a side effect, this statement will evaluate to 0 when there are no numbers left in the file, which in turn causes us to exit the while loop when we reach the end of the input file.
To write the contents of an int array A containing N items to a text file we use the following code.
std::ofstream out; // Declare an ofstream object
out.open("output.txt"); // Open the file
for(int n = 0;n < N;n++)
out << A[n] << std::endl; // Write the numbers
out.close(); // Close the file
In a minute we are going to see a program that reads a list of ints from a text file into an array. After reading, we will want to sort the numbers in the array into ascending order. Here is the code for an elementary sorting algorithm, insertion sort.
void sort(int A[],int N)
{
for(int n = 1;n < N;n++) {
int mover = A[n];
int k = n;
while(k > 0) {
if(A[k-1] > mover) {
A[k] = A[k-1];
k--;
} else
break;
}
A[k] = mover;
}
}
This algorithm works its way systematically through all of the items in the array trying to put each item in the correct location. The main loop iterates through the items using an index n. On each iteration of the main loop, the algorithm takes the item found at location n in the array (called the mover) and attempts to insert it into the correct location. The algorithm does this by comparing the mover with each of the items before it in the array. The algorithm uses an inner loop with index k to iterate over the items from position n-1 down to position 0. If the mover is smaller than the item in location k-1, we move that item one space to the right to create a gap. As soon as we encounter an item which is less than or equal to the moving item, we stop and drop the moving item into the last gap we created.
Here now is the source code for the first version of our number sorting program.
#include <iostream>
#include <fstream>
// Sort the array using insertion sort
void sort(int A[],int N)
{
for(int n = 1;n < N;n++) {
int mover = A[n];
int k = n;
while(k > 0) {
if(A[k-1] > mover) {
A[k] = A[k-1];
k--;
} else
break;
}
A[k] = mover;
}
}
int main (int argc, const char * argv[])
{
std::ifstream in;
std::ofstream out;
int N = 100;
int n = 0;
int k;
int* A = new int[N];
in.open("numbers.txt");
int x;
while(in >> x) {
// Resize the A array if needed.
if(n == N) {
int* B = new int[2*N];
for(k = 0;k < n;k++)
B[k] = A[k];
delete[] A;
A = B;
N *= 2;
}
A[n] = x;
n++;
}
in.close();
std::cout << "Read " << n << " integers from the file." << std::endl;
sort(A,n);
out.open("sorted.txt");
for(k = 0;k < n;k++)
out << A[k] << std::endl;
out.close();
delete[] A;
std::cout << "Done sorting and saving." << std::endl;
return 0;
}
There is one further special thing going on here that we need to comment on. Because we don't know how many numbers are going to be in the text file, we have to proceed by creating an array to start with and then resizing it as we need more room. The process starts by creating an initial array of 100 ints:
int N = 100; int* A = new int[N];
Inside the loop that reads the numbers, we put the following code:
// Resize the A array if needed.
if(n == N) {
int* B = new int[2*N];
for(k = 0;k < n;k++)
B[k] = A[k];
delete[] A;
A = B;
N *= 2;
}
This code starts with a test that checks to see whether or not the A array has just run out of space. If it has, we respond by creating a new array of ints with room for twice as many numbers. We copy the numbers from A over to this new array, destroy the old array that A used to point to, and finally make A point to the new array we created.
Switching from indices to pointers
In the first version of our sorting program we have already made some limited use of pointers in the array creation process. Once the array we created, we switched to the more conventional array index notation to work with the array.
Standard pointer operations make it possible to do everything we can do with integer indices and the standard bracket notation. A little later in this lecture I will fully convert the sorting program we developed above into a program that uses points for all of its logic.
Before we do that, let's start by looking at a simple example of a conversion from array notation to pointer notation. Here is a function that does a linear search to determine whether or not a given item appears in an array.
// Return the first index where x appears, or N if it does
// not appear in the array A.
int search(int A[],int N,int x) {
int k = 0;
while(k < N) {
if(A[k] == x)
return k;
else
k++;
}
return N;
}
Here is the same function implemented purely with pointers.
// Return a pointer to the first location where x appears, or
// end if it does not appear anywhere in the range bounded by
// the pointers begin and end.
// This function assumes that begin points to the first item to
// search and that end points just past the last item.
int* search(int *begin,int *end,int x) {
int* ptr = begin;
while(ptr != end) {
if(*ptr == x)
return ptr;
else
ptr++;
}
return end;
}
Here now is the insertion sort algorithm rewritten to use pointers instead of conventional array indices.
// Sort the items between begin and end.
// end should point just past the end of the
// range of values being sorted.
void sort(int *begin,int *end)
{
// Sort the array using insertion sort
int *mover = begin; // mover points to the element being inserted.
mover++;
while(mover != end) {
int value = *mover; // The value of the item being inserted
// The current pointer will scan through the part of the array
// that appears before the mover location.
int *current = mover;
while(current != begin) {
// previous points to the location before current
int *previous = current;
previous--;
// As long as we keep seeing numbers that are greater than
// the value we are inserting, we will keep moving things
// aside to make room for the value we want to insert.
if(*previous > value) {
*current = *previous;
current--;
} else
break;
}
// Drop the value into place and move on to the next
// item to insert.
*current = value;
mover++;
}
}
The best way to understand what this function is doing is to trace through a simple example by hand. For example, if we use this code to sort an array whose initial contents are {3,4,1,6,5,2}, then part way through the sorting process we will have something that looks like this:
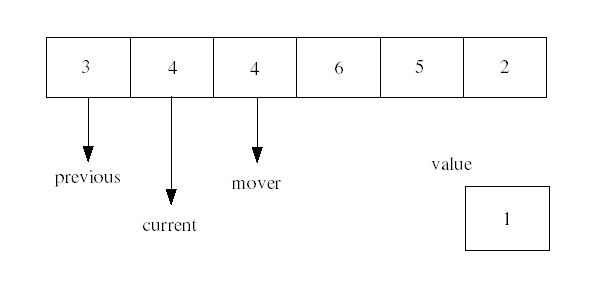 |
To use this function we will use code something like this:
sort(A,A+n);
This code assumes that A is a pointer that points to the beginning of an array. The range that we want sorted is the range of indices [0,n) starting at position 0 and ending just before position n.
Programming Exercise
Here is the full source code for the program that uses the pointer insertion sort function shown above to sort a file of numbers.
Construct a version of this program that uses a different sorting algorithm. Below is code for an alternative sorting algorithm, called selection sort. The strategy that selection sort uses is to search the numbers in a portion of the array for the smallest number it can find. Once it has located that smallest number it moves it to the beginning of the range by making it trade places with the number sitting at the start of the range. On the first iteration of the sorting process we will want to search the entire array from index 0 to index N-1 for its smallest number. On the second iteration of the search process we will want to search the portion of the array between indices 1 and N-1 for the smallest number in that range, because we have already found the smallest number and placed it in position 0. The process continues in this way, with iteration k of the sorting process searching the range of indices from k to N-1 for the kth smallest number in the list.
The selectionSort() function makes use of a helper function swap() that makes two items in A trade places.
// Swap the items in locations i and j
// of the array A.
void swap(int A[],int i, int j)
{
int temp = A[i];
A[i] = A[j];
A[j] = temp;
}
void selectionSort(int A[],int N)
{
for(int k=0; k< N;k++) {
int min = k;
for(int n = k+1; n < N; n++){
if (A[n] < A[min]) {
min = n;
}
}
swap(A,min,k);
}
}
Construct a version of selectionSort that uses pointers in place of integer indices and the standard A[n] notation. Rewrite the program I linked to above to use this sorting algorithm in place of the original algorithm.