Two examples from the textbook

These lecture notes document an extended example of a program that can parse and evaluate algebraic expressions the user enters. This example is based in part on two examples found in the textbook, the recursive descent interpreter of section 5.11 and the expression tree example of section 6.12 (section 6.10 in the third edition). After reading these lecture notes you may want to review those sections in the textbook.

Complete source code for the example

Here is an archive containing the complete source code for this example.

Grammars, Parse Trees, and Parsers

The program we are going to develop in these lecture notes reads and interprets statements in a simple programming language. Here is an example of a typical run of the program.

a = 2
2
b = a + 3
5
a*2 + b - 5
4

Each time the user types a line of input, the program will evaluate that input and print the value that the input evaluates to. The program accepts statements that set up values for variables, and also allows you to type arithmetic expressions that use those variables. The set of valid expressions that users can type in this program are governed by a very simple programming language. The program has the ability to analyse the structure of its inputs and then evaluate them.

All programming languages must follow a set of structure rules - most commonly those structure rules can be expressed via a context-free grammar. A grammar is a set of structure rules that describes how statements in the language can be decomposed into smaller elements, going all the way down to the individual elements in the statement such as numbers, variables, and operators.

Here is the set of grammar rules for the simple language our program will work with.

statement -> assignment | calculation
assignment -> variable '=' sum end
calculation -> sum end
sum -> product (('+' product)|('-' product))*
product -> factor (('*' factor)|('/' factor))*
factor -> power | term
power -> term '^' factor
term -> group | variable | number
group -> '(' sum ')'

Grammar rules are made up grammar variables, terminal symbols, and operators. Each grammar rule consists of a grammar variable, the -> arrow, and a right hand side. Right hand sides consist of one or more grammar expressions connected by operators. The two operators that appear in our example grammar are the or operator, |, and the Kleene star operator, *. The or operator tells us that a grammar variable can expand into one or more alternatives. For example, the grammar rule

factor -> term | power

says that the variable factor can expand to either the term variable or the power variable.

The Kleene star operator says that we can have zero or more instances of something. For example, the rule

product -> factor (('*' factor)|('/' factor))*

says that a product is a single factor followed by 0 or more instances of ('*' factor) or ('/' factor).

Grammar rules are used to construct derivations. In a derivation we start with the grammar's start symbol statement in this example) and apply a series of grammar rules. Each time we apply a grammar rule we use it to replace one of the grammar variables with a new set of variables or terminal symbols.

Here is a concrete example. The expression

3 + 4 * (5 + 2)

is a valid expression in our language. We can prove that the expression is valid by constructing a derivation that starts with the variable statement and ends with something that is equivalent to the text above:

statement => calculation => sum end 
=> product '+' product end
=> factor '+' product end
=> term '+' product end
=> number '+' product end
=> number '+' factor '*' factor end
=> number '+' term '*' factor end
=> number '+' number '*' factor end
=> number '+' number '*' group end
=> number '+' number '*' '(' sum ') end
=> number '+' number '*' '(' product '+' product ')' end
=> number '+' number '*' '(' factor '+' product ')' end
=> number '+' number '*' '(' term '+' product ')' end
=> number '+' number '*' '(' number '+' product ')' end
=> number '+' number '*' '(' number '+' factor ')' end
=> number '+' number '*' '(' number '+' term ')' end
=> number '+' number '*' '(' number '+' number ')' end

A parser is a software program that takes an expression as its input and attempts to construct a derivation for the expression using the available grammar rules. In the example program below I will construct a particular kind of parser known as a recursive descent parser. This style of parser replicates the grammar rules with a set of recursive functions.

Here is the class declaration for the parser class I will use.

class Parser
{
public:
  Parser(char* line);
  ~Parser();

  Expression* statement();
private:
  Tokenizer* tokens;

  Expression* assignment();
  Expression* calculation();
  Expression* sum();
  Expression* product();
  Expression* factor();
  Expression* power();
  Expression* term();
  Expression* group();
  Expression* number();
  Expression* variable();
};

The first thing to note here is that the parser class contains a method for each one of the grammar variables in our expression grammar. The purpose of each one of these methods is to determine whether or not some structure that can be derived from a particular grammar variable is present in the input.

Here is an example of one of these member functions.

Expression* Parser::factor() {
  Expression *exp = nullptr;
  if ((exp=power()) || (exp=term())
    ;
  return exp;
}

This method models the grammar rule

factor -> power | term

The method tries to determine whether or not a valid factor is present by first trying to prove that a valid power is present. If that fails, it will try proving that a term is present instead. The precise mechanism used here takes advantage of the short circuit evaluation rule for the C++ || operator. C++ will evaluate logical ors from left to right, but only until it finds a term that evaluates to true. Once it encounters that true, none of the remaining expressions in the or will get evaluated. This code leverages that behavior in a subtle and important way. The or expression in the if first calls power(). If power() returns a value other than nullptr (which indicates success), we will assign that value to exp. The side-effect of the assignment is to evaluate to the value assigned, which in this case is the pointer value. Since the pointer value is not nullptr, it evaluates to true, short-circuiting the or before we get a chance to try calling term(). If, on the other hand, power() had returned nullptr, the first clause in the or would have evaluated to false, which forces us to go ahead and try the second clause. The second clause calls term(), which may now return a pointer to a valid object.

The Parser class constructor takes a single parameter, a pointer to an array of characters containing the input expression. The constructor will use that text to initialize a second object, a Tokenizer. The purpose of the tokenizer is to break the input into distinct chunks, called tokens. The tokens correspond to the terminal symbols in the grammar. The example grammar we are using here has four terminal symbols, number, variable, end and various characters.

Here is an example of a method in the Parser class that uses the Tokenizer to look for tokens of a particular type.

Expression* Parser::assignment()
{
  int mark = tokens->mark();
  VariableExpression *var = nullptr;
  Expression *rhs = nullptr;
  if ((var=tokens->variable()) && tokens->character('=') && (rhs=sum()) && tokens->atEnd()) 
    return new AssignmentExpression(var, rhs);
  if (var)
    delete var;
  if (rhs)
    delete rhs;
  tokens->reset(mark);
  return nullptr;
}

This method corresponds to the grammar rule

assignment -> variable '=' sum end

In this rule, sum is a grammar variable, while variable and end are terminal symbols. Notice how the method uses the variable() method in the tokenizer to determine whether or not this element is present at the current location in the input.

Beyond simply determining whether a particular structure is present in the input, the parser methods also have an important side effect. Each time one of the parser methods finds a valid structure, it will construct an expression tree that contains information about the structure. The structure trees in this example are made up of Expression nodes. If one of the parser methods fails, it will signal failure by returning nullptr instead of a pointer to an expression tree.

The parser class also has the ability to backtrack out of failed parses. Some grammar rules require us to find several structures in a sequence. If we make it partway through that sequence before failing, we will have to back up to an earlier point in the input and try a different alternative. The assignment() example from above shows how this works.

Expression* Parser::assignment()
{
  int mark = tokens->mark();
  VariableExpression *var = nullptr;
  Expression *rhs = nullptr;
  if ((var=tokens->variable()) && tokens->character('=') && (rhs=sum()) && tokens->atEnd()) 
    return new AssignmentExpression(var, rhs);
  if (var)
    delete var;
  if (rhs)
    delete rhs;
  tokens->reset(mark);
  return nullptr;
}

To make a complete assignment we need to see a variable, the '=' symbol, a complete sum, and the end of the input. If we don't see all of those things, we have to delete any partial expressions we constructed along the way and reset the Tokenizer back to the state it was in when we began the process.

The mechanism for resetting the input works through the mark() and reset() methods in the Tokenizer class. The mark() method returns an int that tells us our present position in the input string. By saving this location and eventually passing it back to the reset() method in case of failure, we can reset the Tokenizer back to its prior location so that the parser can try an alternative route.

The example above also illustrates the short-circuit behavior of the logical and in C++. In C++ logical and expressions get evaluated from left to right until one of the expressions evaluates to false. At that point, all evaluation stops and the entire and expression evaluates to false. This short-circuit behavior is important for a parser, because as soon as the parser sees something that is out of place it should stop trying and reset back to the previous location. For example, the assignment() parser method above will immediately stop if the first element encountered is not a variable.

Expression trees

When the parser succeeds in finding a valid derivation for a particular input string it will respond by constructing an expression tree for the input expression. For example, we determined above that the input expression

3 + 4 * (5 + 2)

is a valid expression in our language by constructing a valid derivation. Here is a picture of the expression tree the parser methods will return at the conclusion of the parse:

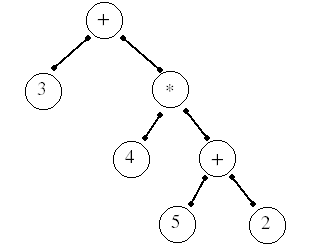
The tree we will end up constructing after a valid parse is an example of a heterogeneous structure. A heterogeneous structure is a data structure made up of nodes held together by pointers, but the nodes are not all of the same type.

This raises an obvious problem. Since many of the nodes in the tree structure need to point to child nodes, how can we set up those pointers if we don't know what type of thing the children will be?

The way out of this problem is to use a powerful combination of C++ language features, inheritance and polymorphism.

We start by making a base class for expression nodes, the Expression class:

class Expression
{
public:
  Expression();
  virtual ~Expression();

  static void initVars();
  static double lookUp(const std::string& var);
  static void record(const std::string& var, double value);

  virtual double evaluate() = 0;
protected:
  static std::map<std::string, double> vars;  
};

We then make a series of more concrete classes that inherit from this base class, the NumberExpression, VariableExpression, ArithmeticExpression, and AssignmentExpression classes. For example, here is the declaration for the ArithmeticExpression class:

class ArithmeticExpression : public Expression
{
public:
  ArithmeticExpression(char op, Expression *left, Expression *right);
  virtual ~ArithmeticExpression();

  virtual double evaluate();
private:
  Expression *left, *right;
  char op;
};

The syntax ArithmeticExpression : public Expression says that the ArithmeticExpression class inherits from the Expression class. In this relationship we say that the Expression class is the base class and ArithmeticExpression is the derived class.

Note also that the ArithmeticExpression class naturally contains two pointers to children. Those pointers are declared as pointers to Expression objects. Since all of the derived classes such as NumberExpression or VariableExpression derive from Expression, a pointer to any one of these types counts as a pointer to a valid Expression object.

An important part of the declaration of the Expression class is this line:

virtual double evaluate() = 0;

This declaration sets up a special kind of member function, called a virtual function. Virtual functions work hand in hand with inheritance heirarchies and help solve some of the problems raised by using pointers to base classes. Consider the following example:

Expression *lhs = new NumberExpression("2");
Expression *rhs = new NumberExpression("3");
Expression *exp = new ArithmeticExpression('+',lhs,rhs);
double value = exp->evaluate();

First of all, this code is valid, because an ArithmeticExpression is technically also an Expression, so we can store a pointer to an ArithmeticExpression in the variable exp. The interesting behavior comes when we do exp->evaluate(). When the compiler encounters this code, it will start by checking to see if the Expression class contains an evaluate() method. The Expression class does contain such a method, and furthermore that method is declared virtual. When a method is declared virtual, the system will figure out the actual type of the object that exp points to and call the version of the evaluate() method that is appropriate for that type of object. In this example exp actually points to an ArithmeticExpression object, so we will end up calling the ArithmeticExpression version of the virtual function.

As you can see from the class declaration above, ArithmeticExpression contains an overload of the evaluate() method, so the virtual function mechanism will correctly call that version of evaluate() instead of the version found in the Expression class. Furthermore, since every class that derives from the Expression class will have its own override of the evaluate() method, the Expression class does not even need a version of this method. In fact, what the declaration

virtual double evaluate() = 0;

actually says is that evaluate() is a virtual method in the Expression class, but we will not be providing an implementation of that method. Instead, every single one of the derived classes will provide its own version of evaluate().

Virtual functions make some very powerful behavior possible. Here is the code for the ArithmeticExpression class's version of the evaluate() method:

double ArithmeticExpression::evaluate() {
  if (left == nullptr || right == nullptr)
    return 0;

  double result = 0;
  double a = left->evaluate();
  double b = right->evaluate();
  switch (op) {
  case '+':
    result = a + b;
    break;
  case '-':
    result = a - b;
    break;
  case '*':
    result = a * b;
    break;
  case '/':
    result = a / b;
    break;
  case '^':
    result = std::pow(a, b);
    break;
  }
  return result;
}

The ArithmeticExpression class contains two child pointers, left and right. Both of those pointers are declared to be pointers to Expression objects. In practice, those pointers will point to objects that could have any one of a number of different types, such as NumberExpression, VariableExpression, or ArithmeticExpression. When the code above calls the evaluate() method on the two children, the virtual function mechanism will automatically call the correct version of the evaluate() method for each of the two children, so we don't have to worry about what kinds of objects the children actually are.

Another place where virtual functions are used in destructors. Here is the destructor for the ArithmeticExpression class:

ArithmeticExpression::~ArithmeticExpression() {
  if (left)
    delete left;
  if (right)
    delete right;
}

This method calls delete on the two child pointers, which in turn causes the destructors for those child objects to run. If you look back at the declaration of the Expression and ArithmeticExpression classes above you will see that the destructor in the Expression class is declared virtual. Once again, this makes it possible to automatically select the correct destructor when we call delete on one of the child pointers.

Programming Assignment

In this assignment you are going to extend the simple language that the program can handle to include function calls. To do this, you will add two new capabilities to the underlying language: the ability to define a function and the ability to call that function once it is defined. Here is an example of a program run to illustrate how this will work:

f(x) = x^2 + 1
0
f(3)
10
f(f(1))
5
a=1
1
b=0-2
-2
f(a+b)/f(a-b)
0.2

The first evaluation defines a new function, f(x), and the subsequent evaluations demonstrate that function being called.

To add this capability to the program you will need to do the following things:

1. Create two new subclasses of the Expression class, FunctionCallExpression and FunctionDeclareExpression.
2. Add additional parser methods to the Parser class to recognize function declarations and function calls.
3. Add a second static map to the Expression class. You will use this map to store the definitions of functions. Each entry in the map will store the parameter name used when the function was defined, along with a pointer to an Expression. That pointer will point to the expression on the right hand side of the original function definition.
4. Add a new virtual method double substitute(std::string var,double value) to the Expression class and its derived classes. This method will evaluate the expression while substituting the given value for the variable whose name is var.
5. The evaluate() method for the FunctionCallExpression class will carry out the following steps:
1. It will call evaluate() on the argument to the function to produce a value.
2. It will look up the entry for the function in the static map that stores function definitions.
3. It will call substitute() on the body of the function definition to replace the parameter name given in the original definition with the value computed in step 5.1 above.
4. It will return the result of the substitution as its result.

Here is some further detail on how the function definition and function call procedures should work.

We start by typing in a function definition:

f(x) = x^2 + 1

f in this example is the name of the new function, and x is its formal parameter. The expression x^2+1 becomes the body of the function.

When the parser parses this expression, it will make a FunctionDeclareExpression that stores the function name, the name of the formal parameter, and a pointer to the body expression. Calling evaluate() on this object will cause it to place a new function definition in the map. It does this by placing a new entry in the function map at the function name. This new entry is a pair that stores the name of the formal parameter and a pointer to the body expression.

Next, we type an expression containing a function call:

1/f(2/10^2)

When the parser encounters the function call, it will make a FunctionCallExpression object for the function call. Evaluating the resulting expression will eventually cause us to call evaluate() on that FunctionCallExpression object. evaluate() will then do the following:

1. It evaluates the argument to the function call to a double, 0.02.
2. It looks up the definition of the function f. That definition says that the formal parameter for f is x and the body of f is x^2+1.
3. It then calls substitute() on the body of f, telling it to replace x with the actual parameter, 0.02. This evaluates to 1.0004.
4. evaluate() returns 1.0004 as its result.

After fully evaluating the expression we entered, the calculator then returns a final result of 0.9996.