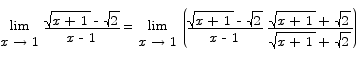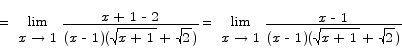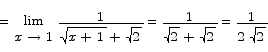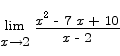
Problem 1 Compute the limit
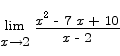
Solution
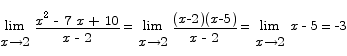
Problem 2 Sketch the graph of the function
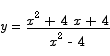
Be sure to include information about horizontal and vertical asymptotes.
Solution The first thing to do here is to factor the numerator and the denominator.
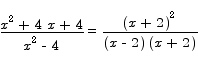
The denominator vanishes at the points x = 2 and x = -2, so we have to investigate these points for potential vertical asymptotes. Near the point x = 2 we can safely cancel the factors of x + 2 that appear in the numerator and denominator, leaving us to understand what the function
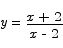
does to either side of x = 2. For x just to the left of 2 we have
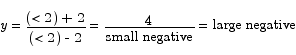
Just to the right we have
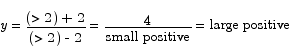
Thus
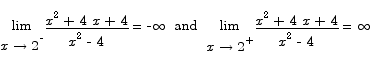
Close to x = -2 we have
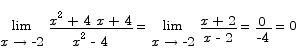
To compute the behavior of the function at infinity we can compute
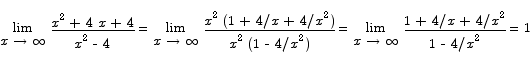
Thus the function approaches a horizontal asymptote of y = 1 at infinity (and also at negative infinity). Putting this all together we can sketch a plot:
 |
 |
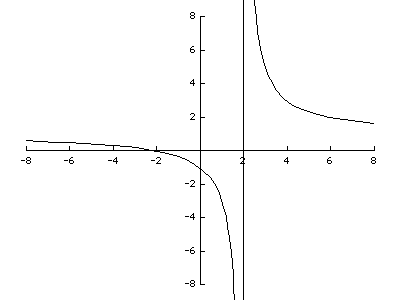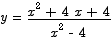Problem 3 Prove that the function
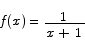
is continuous at each point in its domain. In computing any limits that need to be computed here you may take as given that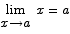 
and 
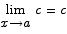for any constant c.
Solution The domain of this function is all points with the exception of x = -1. Let a be any point in the domain. Note that
. 
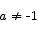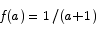
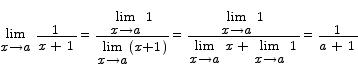
Problem 4 Use the limit rules
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
to prove that
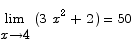
Solution A combination of rules (2) and (6) shows that
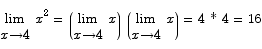
Rule (5) allows us to say
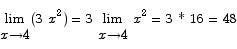
Finally, rule (1) combined with rule (6) gives
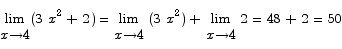
Problem 5 State the intermediate value theorem.
Solution Let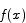 
be a continuous function on the interval [a,b]. If m is any value between 
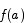and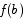 
, inclusive, there must be at least one point c in the interval [a,b] such that 
.
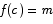Problem 6 Solve the equation
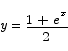
for x.
Solution The first step is to isolate the factor of ex.
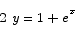
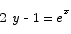
Once that is done, you can solve for x by taking a natural log on both sides.
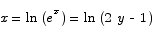
Problem 7 Compute the equation of the tangent line to the graph of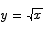 
at the point (4,2).
Solution First we need to compute the slope of the tangent line. To compute that slope we have to use the derivative:
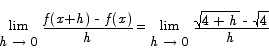
We can use some algebra to compute this limit.
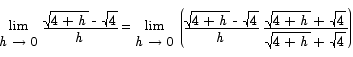
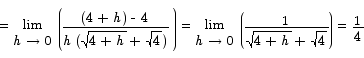
Using the point slope formula we get that the equation of a line passing through (4,2) with slope 1/4 is
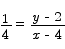
or
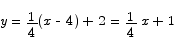
Problem 8 Use the intermediate value theorem to prove that the equation
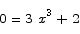
has a solution for some x.
Solution Consider the function
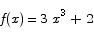
This is a polynomial function and thus is continuous for all x. Note that
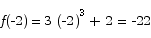
and
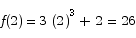
Since f(x) is continuous on the interval [-2,2], the intermediate value theorem says that f(x) must pass through every y value between y = -22 and y = 26, including y = 0. This proves that there is at least one x in the interval [-2,2] where f(x) = 0.
Problem 9 Is the function
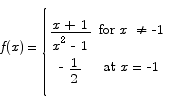
continuous at x = -1?
Solution:
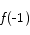is defined (it has value -1/2)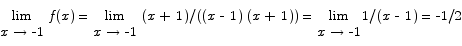
Points 1 and 2 agree, so we see that the function is continuous at x = -1.
Problem 10 Compute the limit
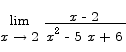
Explain your reasoning clearly.
Solution: By algebra (factoring) we have
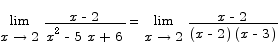
We can cancel terms and then evaluate the limit:
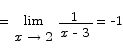
Problem 11 What modification would you need to make to the function
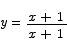
to make it continuous on the entire real line? Explain your reasoning.
Solution: The function is undefined at x = -1. Everywhere else it is defined and has value 1. Clearly, to make it continuous we need to define f(-1) = 1.
We then verify the three points in the definition of continuity at any x. (1) f(a) is now defined for all a (and equals 1 for all a). (2)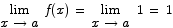 
. (3) The values of points (1) and (2) agree. Thus we can say that the modified f is continuous on the entire real line.
Problem 12 Explain what is wrong with this argument: consider the function
f(x) = 1/x
At x = -1, f(-1) = -1. At x = 1, f(1) = 1. We conclude that at some point c in the interval [-1,1] we must have f(c) = 0.
Solution: The person making this argument seems to be using the Intermediate Value Theorem. This is not a legitimate argument to make, because the function is not continuous everywhere on the interval [-1,1]. (The function is not defined at x = 0.) Not only is the argument not legitimate, but the claim itself is false. The function 1/x is actually never equal to 0.
Problem 13 Use the definition of continuous function along with the relevant properties of limits to prove the following:
Theorem If f(x) is continuous at every point in the interval [c,d], then the function g(x) = x f(x) is also continuous at every point in the interval [c,d].
Solution: Let a by any point in the interval [c,d]. We verify the three points in the definition of continuity of g(x) at a, taking as given the continuity of f(x) at a.
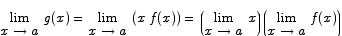. Since f is continuous at a, both limits exist and hence the limit of g exists. (Here we used the result that says that if two limits exist then the limit of the product is the product of the limits.)Since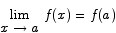 
, we have that 
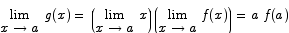, and points 1 and 2 agree.
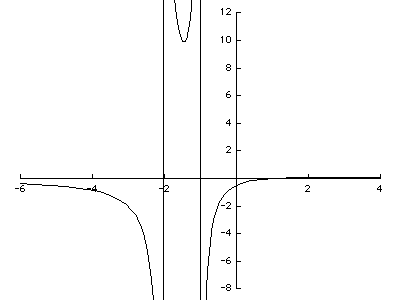
Problem 1 (20 points) Sketch the graph of the function
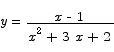
Be sure to include information about horizontal and vertical asymptotes.
Solution After factoring the denominator we see
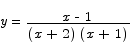
giving us vertical asymptotes at x = -2 and x = -1. For x just to the left of -2 we have
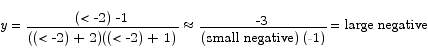
To the right of -2 we have
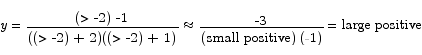
To the left of -1 we have
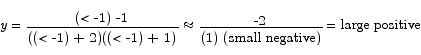
and to the right of -1,
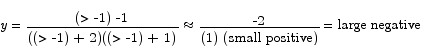
For the limit at infinity,
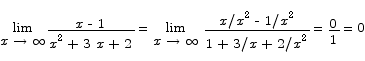
Likewise,
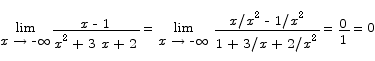
Finally, note that it is easy to see that the only point at which y = 0 is x = 1. Putting this all together we have a graph:
 |
 |
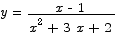Problem 2 (20 points) Use the limit rules
| (8) |
| (9) |
| (10) |
| (11) |
| (12) |
| (13) |
| (14) |
and the definition of continuity to prove that the function f(x) = x2 is continuous for all x.
Solution We check that the three parts of the definition are satisfied for this function.
1. f(a) is defined for all a. Clearly, f(a) = a2. Since this function does not involve square roots of negative numbers, potential division by zero, or any of the other problems that may make functions be undefined, we can say that the function is defined for all a.
2. 
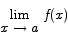exists for all a. To prove that the limit exists, note first that by property [2] we have
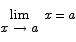
Applying rule [6] gets us that
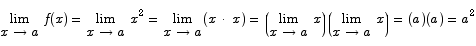
Thus the limit exists for all a.
3. 
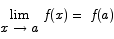for all a. We just showed this in step 2 above.
Thus all three parts of the definition of a continuous function are satisfied at every point a, so f(x) is continuous for all x.
Note We proved a theorem in class that says that all polynomials are automatically continuous everywhere. The problem here was to prove continuity directly from the definition, so you could not use that theorem for this problem.
Problem 3 (20 points) Compute the equation of the line tangent to the graph of y = 1/x at the point (2,1/2).
Solution We begin by computing the slope of the tangent line at x = 2:
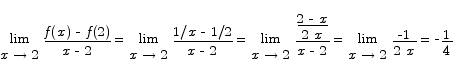
A line with slope -1/4 passing through (2,1/2) has equation
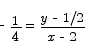
or
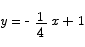
Problem 4 (10 points) Solve the equation
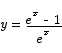
for x.
Solution The proper strategy here is to first isolate the ex term on one side and then take logs on both sides.
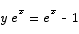
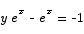
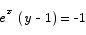
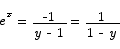
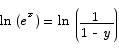
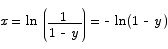
Note A very common mistake that people made on this problem was to improperly distribute the log over a sum or a product. For example, these two are not true:
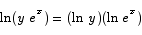
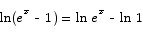
In the first case, the correct result is
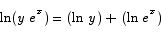
In the second case, there is no way to expand or simplify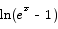 
further.
Problem 5 (10 points) Compute the limit
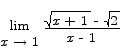
Solution Evaluating the limit directly by setting x = 1 produces 0/0. That means that we have to do some algebra to eliminate the 0/0 problem.
