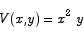
The third midterm exam will cover all of the sections in chapter 4 that we covered in class. Major topics will include
The sample questions below are somewhat light on graphing samples. I am showing fewer of those because I already showed several examples in class. Please see the lecture notes for those examples.
1. Postal regulations stipulate that the combined height and girth (perimeter of the base) of a rectangular package must not exceed 108 inches total. Find the volume of the largest package with a square base that meets this restriction.
Solution If the base of the package has sides of length x and the height of the package is y the volume is given by
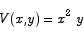
We want to maximize the volume subject to the constraint that girth plus height is 108:
4 x + y = 108
Solving the constraint equation for y gives
y = 108 - 4 x
Substituting this into the volume formula gives
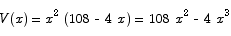
To find the critical point(s) we compute the derivative and set it equal to 0:
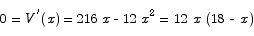
There are two critical points: one at x = 0 (which is uninteresting) and the other at x = 18. Applying the second derivative test to the x = 18 critical point shows that the function is concave down at that point and that it is a maximum.
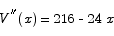
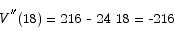
Thus, the volume of the largest package we could send is
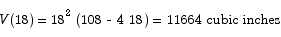
2. Graph the function y = x3 - 2 x + 4. Discuss behavior at infinity, critical points, and concavity. (Note that simply sketching the graph will only get you partial credit - you need to show your work as well.)
Solution
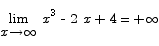
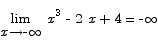
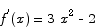. It is easy to see that for x2 < 2/3 the first derivative is negative and for x2 > 2/3 the first derivative is positive. Critical points are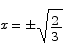
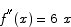. The function has an inflection point at x = 0. For x < 0, the graph is concave down, and for x > 0 the graph is concave up. |
 |
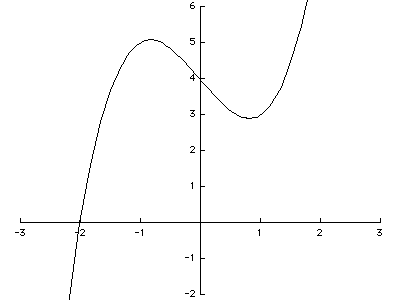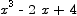3. Show that among all rectangles with a given area the square has the shortest perimeter.
Solution: the quantity we are trying to minimize here is the perimeter of a rectangle with dimensions h by w.
P(h,w) = 2 h + 2 w
The constraint is that the area is fixed.
A = h w
We can use the constraint to solve for h in terms of w:
h = A/w
So that the function to minimize is
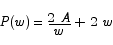
Solving for the critical point we get
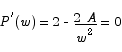
which implies
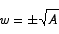
Only the positive root makes sense in this setting. To check that this is a minimum point, we use the second derivative test.
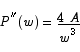
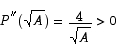
The critical point is a minimum point. Finally, we see that the rectangle with the shortest perimeter is a square because
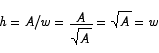
4. Suppose that it costs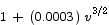 
dollars per mile to operate a truck at v miles per hour. If there are additional costs (such as the driver’s pay) of $10 per hour, what speed should the truck drive at in order to minimize the cost of a 1000 mile trip?
Solution The cost of the trip is
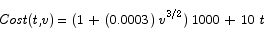
where v is the speed and t is the time spent driving. We can reduce this to a single variable by noting that
1000 = v t
or
t = 1000 / v
Thus the cost function to be minimized is
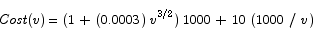
The critical point is
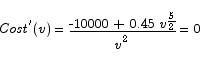
which has solution
v = 54.79172765057419
To check that this is the minimum we can use the first derivative test.
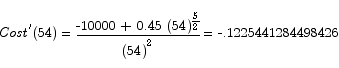
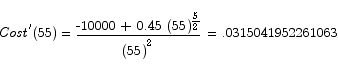
This shows that the critical point is a minimum point. We have to drive the truck at roughly 55 miles per hour.
5. Find the dimensions of the cylindrical can with a volume of 400 cm3 that can be made from the least amount of material possible. (The surface area of a cylinder with base radius r and height h is 
Solution We want to minimize the amount of material needed to make the can, so we need to minimize the surface area.
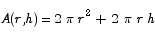
The constraint is that the can must have a volume of 400 cm3:
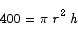
Solving the constraint for h and substituting into the area formula gives
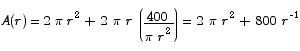
The critical point is located at
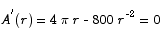
or
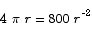
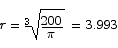
To determine whether or not this corresponds to a minimum, we substitute into the second derivative.
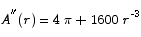
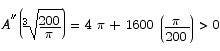
Thus the critical point is a minimum point, as desired. The optimum dimensions are thus
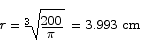
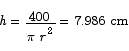
These dimensions are for a can whose base diameter is equal to its height.
6. Compute the limit
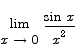
Solution Since both the numerator and denominator go to 0, this problem is a candidate for L’Hôpital’s rule.
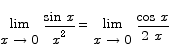
Since the latter goes to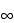 
as x approaches 0 from above and 
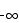as approaches 0 from below, there is no limit in this case.
7. The equation x = 2 sin x has a solution somewhere near 2. Use Newton's method to estimate this solution accurate to ±0.01.
Solution To turn this into a Newton's method problem we have to introduce the function
f(x) = 2 sin x - x
Applying this function to the Newton iteration formula
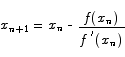
gives
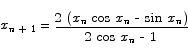
Applying this formula to a starting guess of x0 = 2 gives
| n | xn |
|---|---|
| 0 | 2 |
| 1 | 1.9009955942039094 |
| 2 | 1.8955116453795946 |
| 3 | 1.8954942672087132 |
The solution is somewhere near x = 1.895.
8. Compute
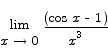
Solution: both the numerator and the denominator go to zero as x approaches 0, so L‘Hôpital’s rule applies to this problem. Differentiating top and bottom we have
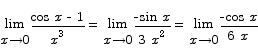
Note that we had to apply L‘Hôpital’s rule a second time. The final limit is indeterminant because as x approaches 0 from below we have a limit of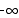 
and as x approaches 0 from above we have a limit of 
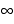. Since these do not agree, there is no limit.
9. Compute the limit
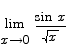
Solution: both numerator and denominator go to 0 as x approaches 0, so this L’Hôpital’s rule applies.
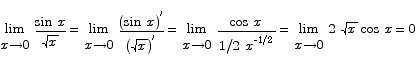
10. Find the value of p that maximizes the function
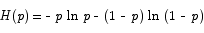
Solution: the derivative of this function is
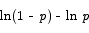
The critical point is located at
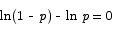
or
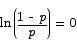
The number whose natural log is 0 is 1, so we are looking for p such that
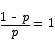
This equation has solution
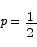
To check that this is a maximum we compute the second derivative.
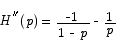
At p = 1/2, this has value -4, so the critical point is a maximum point.
11. Compute the maximum value of the function
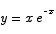
Solution
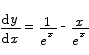
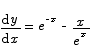
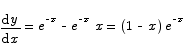
The derivative vanishes when x = 1. It is easy to see that for x less than one this derivative is positive and for x greater than 1 the derivative is negative. This shows that x = 1 is a maximum point by the first derivative test.
12. A triangle is formed from two sides of length a with an interior angle of 
between them. Find the value of 
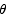that maximizes the area of the triangle.
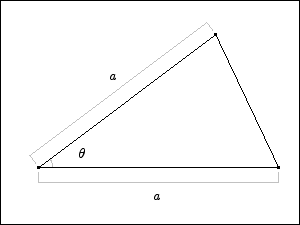
Solution The area of the triangle is 1/2 base times height. The height is the distance from the very top to the base. By simple trig that height is given by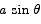 
. Thus the area as a function of 
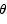is
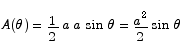
To maximize this we find the critical point.
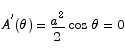
The critical point is located at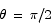 
. To check that this is a maximum point we compute the second derivative.
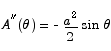
At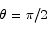 
the second derivative is negative, thus we have a maximum.
13. Use the Mean Value Theorem to prove that if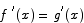 
for all x and 
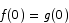then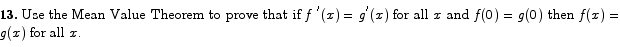 
for all x.
Solution Introduce the function
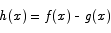
The function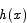 
is 0 at x = 0 and its derivative is 0 for all x. What we have to show about 
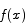and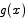 
amounts to showing that 
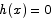for all x. Suppose by contradiction that 
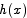was not 0 for all x. Let b be any point at which 
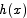is not 0. Apply the MVT with a = 0 and this b to see that there is a c such that
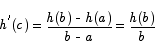
Since by assumption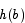 
is not 0, the derivative of h at c is also not 0. This contradicts the fact that the derivative of 
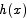is 0 for all x. The only way out of this contradiction is to say that 
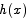is 0 for all x, which amounts to saying that 
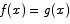for all x.
1. Describe as fully as possible the behavior of the function
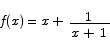
Are there any vertical, horizontal, or slant asymptotes? What is the behavior of the function near those asymptotes? Find all of the critical points and determine where the function is increasing and decreasing. Find inflection points and describe the concavity of the function.
Solution The function has an obvious vertical asymptote at x = -1. As x approaches -1 from below the function becomes very large negative. Just to the right of -1 the function becomes very large positive. The behavior at infinity is dominated by the x term. It is easy to see that as x becomes very large negative or positive the fractional term shrinks to 0 and the function approaches y = x as a horizontal asymptote.
The first derivative of the function is
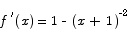
To find critical points we solve
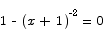
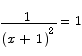
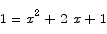
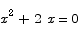
There are critical points at x = 0 and x = -2. The value of the function at the two critical points is
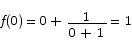
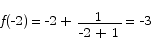
The first derivative is positive for x < -2 and x > 0 and negative for -2 < x < 0. The second derivative is
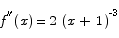
which is negative for x < -1 and positive for x > -1. There are no inflection points.
 |
 |
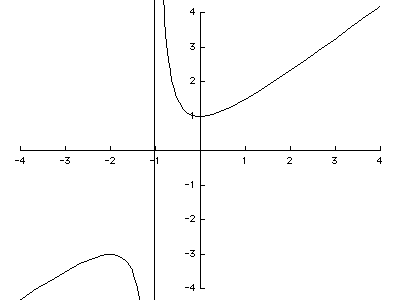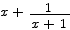2. A fence 8 feet tall runs parallel to the wall of a tall building 4 feet from the building. What is the length of the shortest ladder that will reach from the ground to the side of the building just touching the top of the fence?
The diagram below shows the relevant distances.
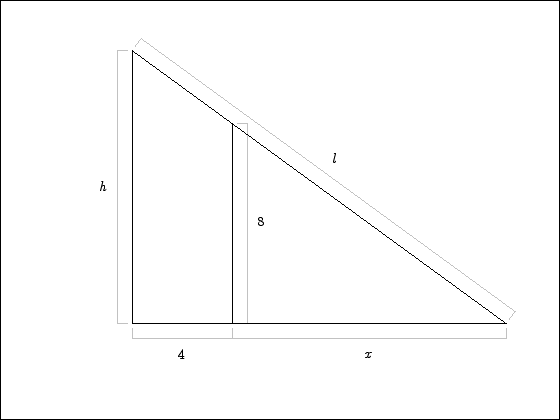
We want to minimize the length l. For convenience, we will minimize l2 instead. By Pythagorus’s theorem we have
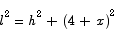
To get a constraint equation we can use a similar triangle argument:
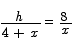
This leads to
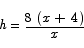
Thus we need to minimize
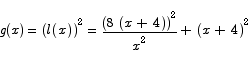
The first derivative is
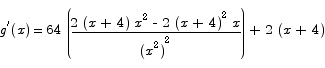
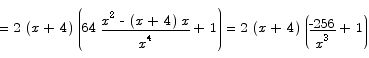
There are two critical points here, x = -4 and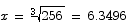 
. The negative critical point is obviously uninteresting. It is easy to see that for 
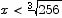the first derivative is negative and that for 
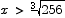the first derivative is positive. Thus the second critical point is a minimum point. The shortest ladder has length
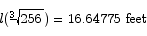
3. Use the Mean Value Theorem to prove that if g(x) is differentiable everywhere and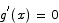 
for all x then g(x) is a constant.
Solution (from the lecture notes) Suppose that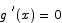 
for all x. By way of contradiction, pretend that g(x) is not a constant function. Since g(x) is not constant, there should exist points a and b for which
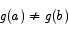
Apply the MVT to points a and b. You get that there is a point c in between a and b for which
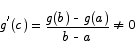
This is a contradiction, so the function must have been constant to start with.
4. The function f(x) = x4 + x - 4 has a root somewhere in the neighborhood of x = 1. Use three iterations of Newton's method starting from x0 = 1 to compute an approximation for that root.
Solution Newton's formula applied to the function
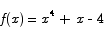
gives the iteration formula
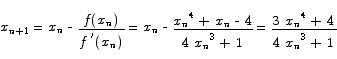
The table shows the result of three iterations of this formula.
| n | xn |
|---|---|
| 0 | 1 |
| 1 | 1.4 |
| 2 | 1.296325985 |
| 3 | 1.283943953 |