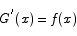
Theorem Let f(x) be a continuous function on the interval [a,b]. Let G(x) be any function with the property that
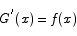
Then
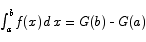
Proof Introduce the area function
| (1) |
By the first fundamental theorem,
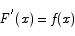
Since F(x) and G(x) have the same derivative, they must differ by a constant.
F(x) = G(x) + C | (2) |
What is that constant? Evaluating equations (1) and (2) at x = a gives us
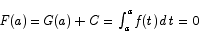
which leads to
G(a) + C = 0
C = -G(a)
Similarly, evaluating the equations at x = b gives
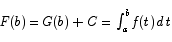
or
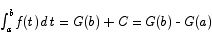
and we are done
Let us now see how the second fundamental theorem gets applied to solve area problems.
Example Compute
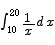
According to the theorem, we need to find a function G(x) with the property
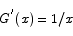
Such a function is called an anti-derivative of 1/x. We can see that one possible solution is
G(x) = ln x
From the theorem
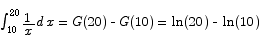
Unfortunately, this anti-differentiation process is not always easy to do.
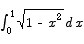
To solve this, we need an anti-derivative
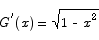
There is no obvious anti-derivative for this function. Given the fact that many anti-derivative problems are hard to do, we will be spending a good chunk of Math 150 working out techniques for computing anti-derivatives.
Since we are going to be computing antiderivatives, one of the first things we are going to need is a convenient notation for antidifferentiation. The notation that is commonly used for the operation of antidifferentiation is called the indefinite integral.
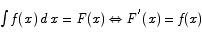
One way to get a start on the problem of computing antiderivatives is to write down the derivatives of some standard functions and then adjust those formulas to make them antidifferentiation formulas.
| f(x) |  |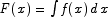
|---|---|
| xn |  |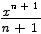
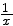 | ln x |
| ex | ex |
| cos x | sin x |
| sin x | -cos x |
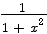 | tan-1 x |
Another useful tool for computing antiderivatives is related to the fact that the derivative of a sum is a sum of derivatives:
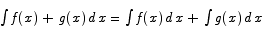
Likewise, since the derivative of k f(x) is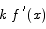 
we have
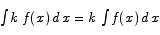
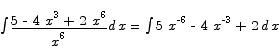
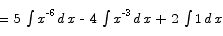
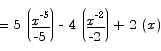
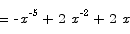
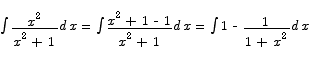
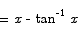
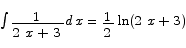
If you want to check whether or not the answer to an antidifferentiation problem is correct, you can always differentiate the answer to see whether or not that returns the original function.
I will not be collecting any more homework problems to grade. These are suggested problems for you to work and check on your own.
Section 4.10: 3, 7, 11, 43
Section 5.3: 19, 21, 35, 47
