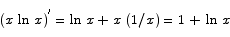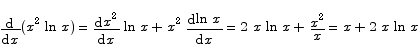
Find the minimum value of the function x2 ln x.
Solution The derivative is
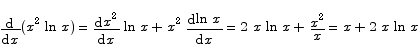
The critical point is
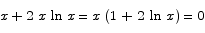
which has two possible solutions. The first of these, x = 0, does not make sense because ln x is not defined at x = 0. The other solution is
ln x = -1/2
or
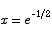
To see that this is the minimum, we compute the second derivative.
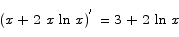
When ln x = -1/2 we have a second derivative of
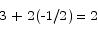
Thus the function is concave up at the critical point and we have a minimum.
Use Newton’s method to estimate the value of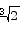 
(the cube root of 2) to four decimal places.
Solution In order to apply Newton’s method, we have to find a function whose root is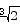 
. Such a function is
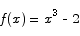
We apply the Newton iteration formula
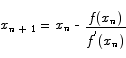
to obtain
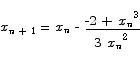
or
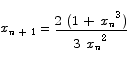
Here is what you get if you apply the iteration with an initial guess x0 = 1.5.
| n | xn |
|---|---|
| 0 | 1.5 |
| 1 | 1.2962962962962963 |
| 2 | 1.2609322247417487 |
| 3 | 1.2599218605659264 |
| 4 | 1.2599210498953948 |
| 5 | 1.2599210498948732 |
The sequence appears to converge rather quickly to an answer of about 1.25992.
Derive the formula A = 1/2 (base)(height) for the area of a right triangle by approximating the area of the triangle with rectangles and taking the limit as the width of the rectangles goes to 0.
Solution The diagram shown here shows the set-up for this problem. We have a right triangle with base a and height b.
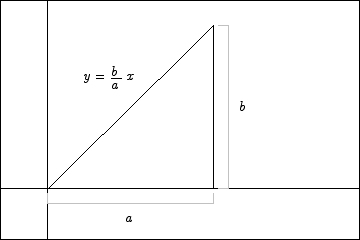
A simple argument shows that the function whose graph is the hypotenuse is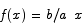 
. If we divide the interval [0,a] into N equal sized sub-intervals each of those sub-intervals will have width a/N. The division points are located at
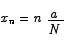
The area of all of the rectangles put together is
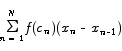
For simplicity, set the sample point in each interval to the right hand endpoint of that interval. The area now is
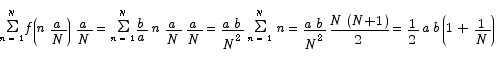
In the limit as N goes to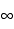 
, the area goes to 1/2 a b.
Use the second fundamental theorem of integral calculus to compute
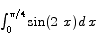
Solution To apply the second fundamental theorem we have to find a function whose derivative is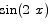 
. It is easy to see that
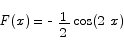
is the anti-derivative we need. By the second fundamental theorem we then have
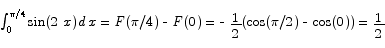
Use the Mean Value Theorem to prove that if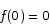 
and 
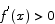for all x, then 
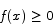for all 
.
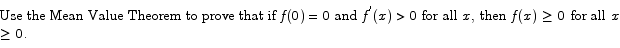Solution Suppose, by way of contradiction, that f(d) < 0 for some d > 0. If we apply the MVT with a = 0 and b = d, we get that there is some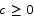 
for which
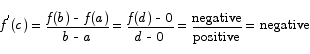
This contradicts the assumption that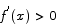 
for all x, so we are forced to conclude that 
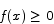for all 
.
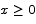Explain why you can not use the second fundamental theorem of integral calculus to compute
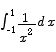
Solution The theorem requires that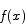 
be a continuous function on the interval [a,b]. 1/x2 is not continuous on the interval [-1,1], so the theorem does not apply.
Compute the derivative with respect to x of
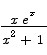
Solution by the quotient rule we have
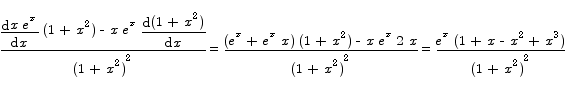
Compute the derivative of ex sin2 x with respect to x.
Solution: ex sin2 x + 2 ex sin x cos x
Set up, but do not evaluate, the sum that estimates the area underneath the semicircle of radius a centered at the origin.
Solution: let us subdivide the interval [-a,a] into n equal sized segments of length (2a)/n. Interval i is the interval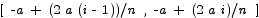 
. Let the height of the rectangle over that interval be given by the height of the function over the right hand end of the subinterval. This gives a height of 
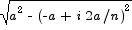. The approximating sum is
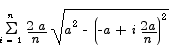
Use the second fundamental theorem of Integral Calculus to evaluate the integral
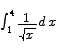
Solution: the antiderivative of the function f(x) = x-1/2 is F(x) = 2 x1/2. Thus
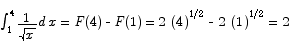
Let f(x) be a continuous function on an interval [a,b] and F(x) the antiderivative of f(x). If xi and xi+1 are any two points in [a,b] with xi < xi + 1, show that there is a point ci,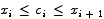 
for which 
.
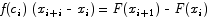Solution: since F(x) is an antiderivative it is differentiable, and hence continuous. We can apply the mean value theorem to F(x) to get that there is a point ci such that
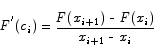
Noting that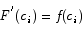 
we have the result to be proved.
Compute the sum
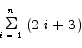
Solution: by standard summation manipulations we have that
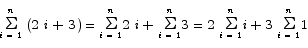
Both of the sums that remain can be evaluated by means of standard summation formulas.
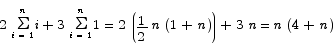
Show that among all rectangles with a given area the square has the shortest perimeter.
Solution: the quantity we are trying to minimize here is the perimeter of a rectangle with dimensions h by w.
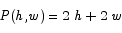
The constraint is that the area is fixed.
A = h w
We can use the constraint to solve for h in terms of w:
h = A/w
So that the function to minimize is
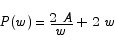
Solving for the critical point we get
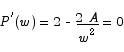
which implies
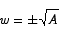
Only the positive root makes sense in this setting. To check that this is a minimum point, we use the second derivative test.
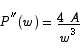
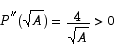
The critical point is a minimum point. Finally, we see that the rectangle with the shortest perimeter is a square because
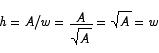
The equation x2 - y2 = 1/9 is the equation of a hyperbola. Find the equation of the tangent line to this curve at the point ( -1/2 ,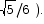 
Solution: we start by computing the derivative via implicit differentiation.
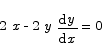
or
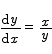
Thus the slope of the tangent line at the point ( -1/2 ,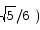 
is
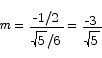
The equation of the tangent line is
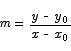
or
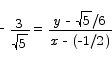
In standard form this is
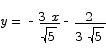
Compute the derivative with respect to x:
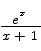
Solution By the quotient rule we have
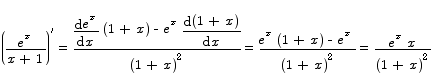
Compute the derivative with respect to x:
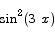
Solution By the chain rule we have
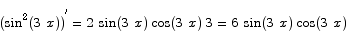
Compute the limit
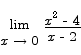
Solution By simple algebra we have
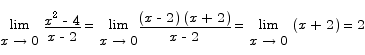
Problem 4 (20 points)
A triangle is formed from two sides of length a with an interior angle of 
between them. Find the value of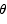 
that maximizes the area of the triangle.
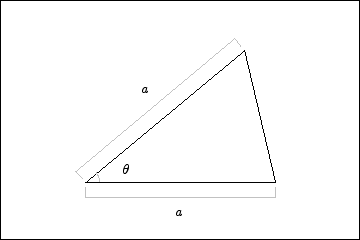
Solution The area of the triangle is 1/2 base times height. The height is the distance from the very top to the base. By simple trig that height is given by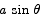 
. Thus the area as a function of 
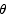is
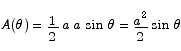
To maximize this we find the critical point.
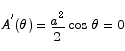
The critical point is located at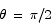 
. To check that this is a maximum point we compute the second derivative.
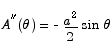
At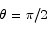 
the second derivative is negative, thus we have a maximum.
Use the second fundamental theorem of integral calculus to compute
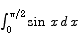
Solution The antiderivative of sin x is -cos x, so
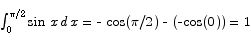
Use Newton's method to solve the equation
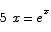
accurate to ±0.01.
Solution We apply the Newton iteration formula
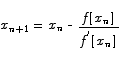
To the function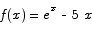 
to obtain the iteration formula
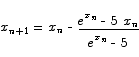
Starting from a guess of x = 1 we obtain
| n | xn |
|---|---|
| 0 | 1 |
| 1 | 0 |
| 2 | 0.25 |
| 3 | 0.25915652567715158 |
| 4 | 0.25917110178191022 |
The solution appears to be x = 0.26.
Compute the summation
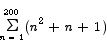
Solution The sum breaks up as three separate terms to which we can apply summation formulas.
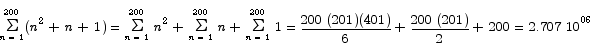
Use the method of implicit differentiation to find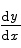 
if
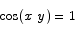
Solution Taking the derivative with respect to x on both sides gives
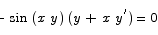
Solving for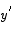 
gives
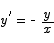
Approximate the area
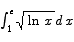
by subdividing the interval [1,e] into 5 equal sized sub-intervals and placing rectangles over those sub-intervals.
Solution The subdivision points are located at
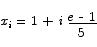
If we make the height of the rectangle over the interval [xi-1 , xi] be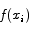 
we have the sum
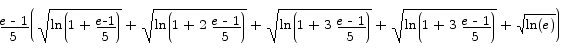
= 1.35752810399109
Use the Mean Value Theorem to prove that if a function is differentiable everywhere and its derivative is equal to 0 everywhere, then the function must be a constant.
Solution Suppose the function is not a constant. Then there must be two points a and b at which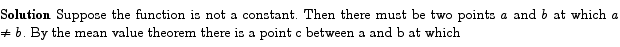 
. By the mean value theorem there is a point c between a and b at which
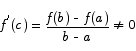
This contradicts the statement that the derivative is 0 everywhere. Hence, the function must take the same value at all points.
Find the maximum value of the function
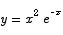
on the interval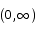 
.
Solution To compute the critical point we compute the derivative:
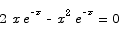
This has two possible solutions, x = 0 and x = 2. Since the first of these is not in the interval we are interested in, we consider the second. To show that x = 2 is a maximum point we can use the second derivative test:
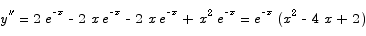
The second derivative is negative at x = 2, thus that critical point is a maximum.
2 - x
Compute the derivative of the function
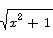
Solution By the chain rule we have
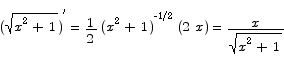
Compute the derivative of the function
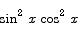
Solution We apply the product rule followed by the chain rule where needed.
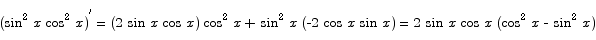
Compute the limit
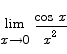
Solution This is not a 0/0 limit, so L’Hôpital’s rule does not apply. As x approaches 0, the numerator approaches 1 while the denominator approaches 0. Since both the numerator and denominator are positive for x on either side of 0, the limit will be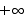 
.
Find the smallest value that the function ex/x takes on the interval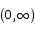 
.
Solution To find the minimum value we compute the first derivative and look for critical points.
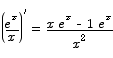
The critical point is located at
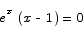
or x = 1. For x less than 1, the first derivative is negative, while for x greater than 1 the first derivative is positive. Thus the critical point x = 1 is a minimum point and
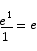
is the smallest value that the function takes.
Compute the value of the sum
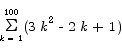
Solution Breaking up the sum and applying the standard summation formulas gives
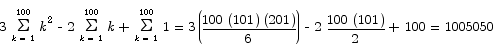
Use the Mean Value Theorem to prove that if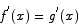 
for all x and 
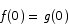then 
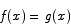for all x.
Solution Introduce the function
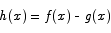
The function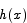 
is 0 at x = 0 and its derivative is 0 for all x. What we have to show about 
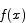and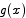 
amounts to showing that 
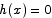for all x. Suppose by contradiction that 
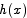was not 0 for all x. Let b be any point at which 
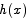is not 0. Apply the MVT with a = 0 and this b to see that there is a c such that
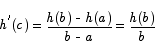
Since by assumption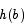 
is not 0, the derivative of h at c is also not 0. This contradicts the fact that the derivative of 
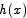is 0 for all x. The only way out of this contradiction is to say that 
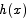is 0 for all x, which amounts to saying that 
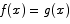for all x.
Estimate the area underneath the graph of y = sin x between x = 0 and x = 1 by dividing the interval into five intervals of equal width and placing rectangles over each of those sub-intervals.
Solution The width of each subdivision is 0.2. Subdivision point xi is located at 0.2 i. For simplicity, let the height of rectangle number i be given by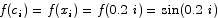 
. The sum of the rectangle areas is
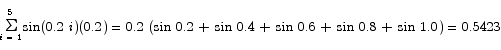
Find the area in problem seven exactly by using the Second Fundamental Theorem of Integral Calculus.
Solution The area to be computed is
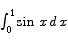
Since the anti-derivative of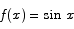 
is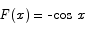 
the second fundamental theorem says
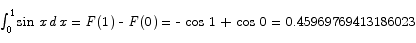
Compute the equation of the line tangent to the ellipse
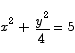
at the point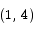 
.
Solution To compute the equation of the tangent line we need to know the slope at that point. To compute the slope we have to use implicit differentiation to compute the derivative.
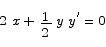
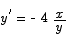
The derivative at the point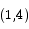 
is
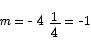
The equation of the tangent line is
y = m x + b = -x + b
To compute b we use the fact that the tangent line passes through the point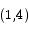 
:
4 = - 1 + b
b = 5
Thus the equation of the tangent line is y = -x + 5.
Let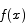 
be a continuous function on the interval [0,1] that has a range of [0,1]. Prove that there must be at least one x in the interval [0,1] for which 
.
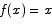Solution If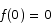 
or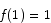 
we are done, so let us assume that 
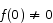and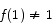 
. Since the range of 
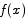is [0,1] this amounts to saying 
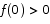and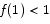 
. Now introduce the function
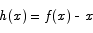
Note that since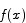 
is a continuous function, 
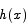is also continuous. Also note that 
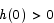and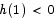 
. By the intermediate value theorem, there must be some point c in the interval [0,1] at which 
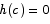. This means that there is a point c such that
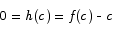
Thus at c we have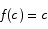 
, which is what we wanted to show.
Show that of all rectangles with a perimeter of 4 the square has the largest area.
Solution We have to maximize area of the rectangle in this problem. The area of a rectangle with base x and height y is
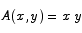
The constraint is that the perimeter of the rectangle must be 4.
4 = 2 x + 2 y
Solving the constraint equation for y and substituting into the area function gives
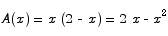
To maximize the area function we find a critical point:
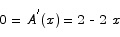
x = 1
To see that the critical point x = 1 is a maximum point we can apply the second derivative test.
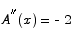
Since the second derivative is always negative, we see that the area function is concave down at the critical point and that x = 1 is a maximum point. The rectangle with the largest area is a square with both sides having length 1.
Compute the derivative of the function
x ln x
Solution By the product rule we have
