An algorithm to evaluate arithmetic expressions
Here is an example program, based on an example from the text, that can evaluate very simple arithmetic expressions.
public class SimpleCalculator {
public static void main(String[] args) {
Scanner input = new Scanner(System.in);
// The result of the operation
int result = 0;
// The original input
System.out.print("Enter an expression to compute: ");
String userInput = input.nextLine();
// The tokens that make up the input
String[] tokens = userInput.split(" ");
// Determine the operator
switch (tokens[1].charAt(0)) {
case '+':
result = Integer.parseInt(tokens[0])
+ Integer.parseInt(tokens[2]);
break;
case '-':
result = Integer.parseInt(tokens[0])
- Integer.parseInt(tokens[2]);
break;
case '*':
result = Integer.parseInt(tokens[0])
* Integer.parseInt(tokens[2]);
break;
case '/':
result = Integer.parseInt(tokens[0])
/ Integer.parseInt(tokens[2]);
}
// Display result
System.out.println(tokens[0] + ' ' + tokens[1] + ' '
+ tokens[2] + " = " + result);
}
}
The program works with very simple arithmetic expressions, such as
34 * 12
The program uses the Scanner class's nextLine method to read the entire line of input that the user types, thus grabbing the entire expression at once. Next, the program uses the String class's split method to split the input into an array of String objects. The middle String in the resulting array contains the operator, so we can use a simple switch statement to process the operator.
Next, we are going to extend this problem to that of evaluating more complex arithmetic expressions. Initially, we are going to see how to handle expressions like
20 - 3 * 6 + 2
Eventually we will extend the basic algorithm to also handle parentheses, making it possible to evaluate expressions like
4 * ( 6 - 2 * ( 4 - 2 ) )
The basic algorithm
We are now ready to see the basic algorithm for computing arithmetic statements without parentheses. The algorithm makes use of two stacks, a value stack and an operator stack.
The basic algorithm processes the tokens from the input in a simple left to right order. Any number tokens that we encounter get pushed onto the value stack. When we encounter an operator token, we will push it onto the operator stack.
At various points in the algorithm we will process an operator. We do this by popping the operator off of the operator stack and popping two numbers off the value stack. We then apply the operator to the two numbers to produce a result, and then push that number back onto the top of the value stack. After the processing is complete, we discard the operator token.
The most important logic in the evaluation algorithm tells us when to process the operators sitting on the operator stack. This logic is driven in part by the precedence of the operators involved: the operators + and - have a precedence of 1, while the operators * and / have a precedence of 2. Here are the key elements of the evaluation algorithm.
- If we encounter an operator token in the input and the operator stack is empty, we push the operator token onto the operator stack.
- If we encounter an operator token in the input with a precedence that is greater than the precedence of the operator token at the top of the operator stack, we push the new operator token onto the operator stack.
- If we encounter an operator token in the input with a precedence that is less than or equal to the precedence of the operator token at the top of the operator stack, we process and remove the operator at the top of the stack. This continues until the operator stack is empty or until an operator with lower precedence than the input operator appears at the top of the stack.
- When we reach the end of the input, any operators that remain on the operator stack are processed and removed until the operator stack is empty. At that point, there should be only one number left on the value stack: that number is the result of the evaluation.
An example
Here is an illustration of this algorithm in action. The expression we want to compute is
2 + 3 * 4 - 6
At the start of the algorithm both stacks are empty and the tokens are lined up in the input.
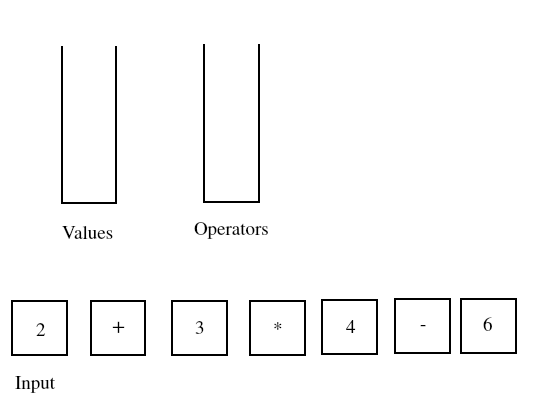
After handling the first three tokens we arrive at this configuration.
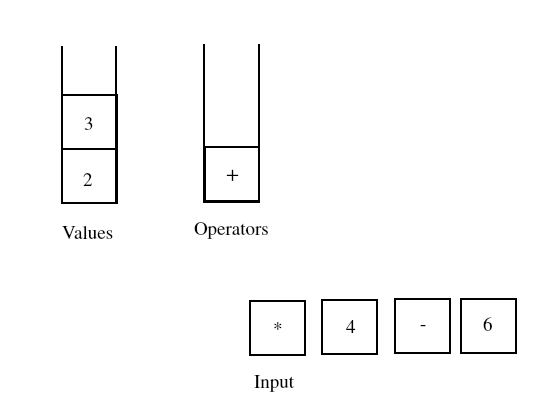
The next operator in the input has a higher precedence than the operator at the top of the operator stack, so we push the next operator. The next number token also gets pushed on the value stack.
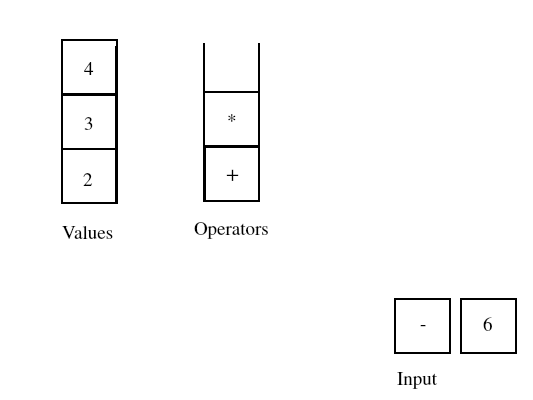
The next operator in the input sequence has a precedence lower than that of the operator at the top of the operator stack. This causes us to process and remove the operator at the top of the operator stack.
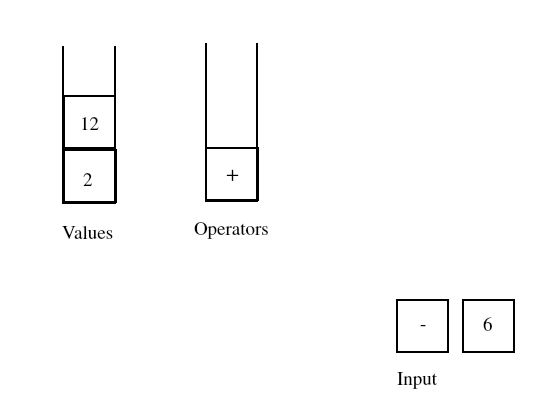
Once again, the operator in the input has a precendence equal to that of the operator at the top of the operator stack, so we process and remove the operator from the operator stack.
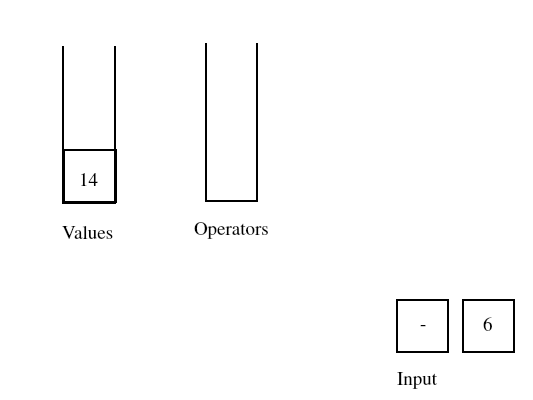
At this point the operator stack is empty, so the operator token at the front of the input gets pushed on the operator stack. The number token at the end of the input gets pushed on the value stack.
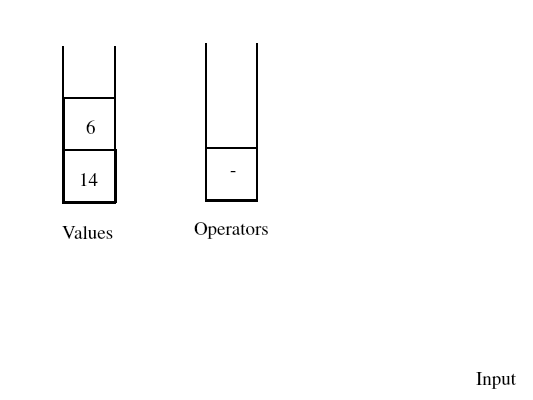
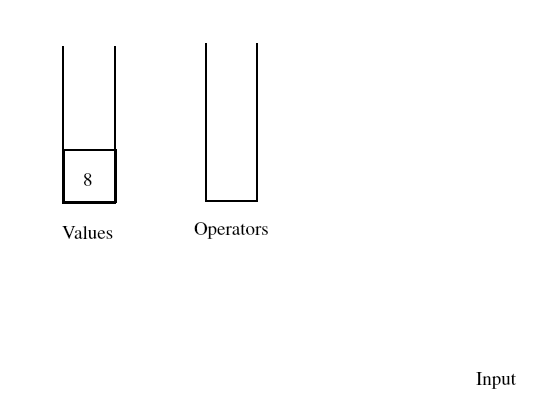
Once the input has emptied out, we process any operators that remain on the operator stack. Once all of those operators have been processed, the sole remaining number on the value stack is the result of the computation.
A generic stack class
In the last lecture I showed a simple stack class. We will need something like that class to implement today's algorithm.
One complication we are going to run into is that we will need two different types of stacks. For the value stack we will need a stack that can store numbers. For the operator stack we will instead need a stack that can store characters. In order to make one stack class work for both types of data, we have instead make our stack class a generic class. In Java a generic class is a class where we replace the data type for at least one of the member variables with a placeholder symbol. This will allow users of our class to make different versions of the basic class by specifying different types to use as the placeholder type.
Here is how this will work in the case of the stack class. The first thing we do is to modify the StackItem class to store a generic value type:
public class StackItem<E> {
public E value;
public StackItem<E> next;
public StackItem(E x) {
value = x;
next = null;
}
}
Then we also convert the stack class to be generic.
public class Stack<E> {
private StackItem<E> top;
public Stack() {
top = null;
}
public void push(E x) {
StackItem<E> newItem = new StackItem<E>(x);
newItem.next = top;
top = newItem;
}
public boolean empty() {
return top == null;
}
public E peek() {
return top.value;
}
public void pop() {
top = top.next;
}
}
With this transformation we can then use the same code to make stacks of doubles and stacks of chars.
Stack<Double> values = new Stack<Double>(); Stack<Character> operators = new Stack<Character>();
Note that just as with the ArrayList class our generic Stack class can only work with object types. Thus, if you want to put doubles on a Stack you have to use the object equivalent type Double. Likewise, in place of the primitive char type we have to use the equivalent object type Character.
Once we have set up the two stacks, we can use the handy Java autoboxing/autounboxing feature to use these classes with the simpler primitive types.
values.push(2.5);
operators.push('*');
For future reference, the Java class library already includes a generic stack class that you can use, the java.util.Stack class.
Handling parentheses
The algorithm outlined above can easily be extended to also handle parentheses correctly. All that is required is a couple of additional rules.
- When we encounter a left parentheses token in the input, we push that token on the operator stack.
- When we encounter a right parenthesis token in the input, we process operators and remove them from the top of the operator stack until a left parenthesis appears at the top of the operator stack. We then pop off the left parenthesis token and discard both of the parenthesis tokens.
The full implementation
With the Stack class described above, we have all of the pieces we need to implement an expression calculator. The last step is to construct a class that can fully implement the algorithm.
public class FullCalculator {
private Stack<Character> operatorStack;
private Stack<Double> valueStack;
private boolean error;
public FullCalculator() {
operatorStack = new Stack<Character>();
valueStack = new Stack<Double>();
error = false;
}
private boolean isOperator(char ch) {
return ch == '+' || ch == '-' || ch == '*' || ch == '/';
}
private int getPrecedence(char ch) {
if (ch == '+' || ch == '-') {
return 1;
}
if (ch == '*' || ch == '/') {
return 2;
}
return 0;
}
private void processOperator(char t) {
double a, b;
if (valueStack.empty()) {
System.out.println("Expression error.");
error = true;
return;
} else {
b = valueStack.peek();
valueStack.pop();
}
if (valueStack.empty()) {
System.out.println("Expression error.");
error = true;
return;
} else {
a = valueStack.peek();
valueStack.pop();
}
double r = 0;
if (t == '+') {
r = a + b;
} else if (t == '-') {
r = a - b;
} else if (t == '*') {
r = a * b;
} else if(t == '/') {
r = a / b;
} else {
System.out.println("Operator error.");
error = true;
}
valueStack.push(r);
}
public void processInput(String input) {
// The tokens that make up the input
String[] tokens = input.split(" ");
// Main loop - process all input tokens
for (int n = 0; n < tokens.length; n++) {
String nextToken = tokens[n];
char ch = nextToken.charAt(0);
if (ch >= '0' && ch <= '9') {
double value = Double.parseDouble(nextToken);
valueStack.push(value);
} else if (isOperator(ch)) {
if (operatorStack.empty() || getPrecedence(ch) > getPrecedence(operatorStack.peek())) {
operatorStack.push(ch);
} else {
while (!operatorStack.empty() && getPrecedence(ch) <= getPrecedence(operatorStack.peek())) {
char toProcess = operatorStack.peek();
operatorStack.pop();
processOperator(toProcess);
}
operatorStack.push(ch);
}
} else if (ch == '(') {
operatorStack.push(ch);
} else if (ch == ')') {
while (!operatorStack.empty() && isOperator(operatorStack.peek())) {
char toProcess = operatorStack.peek();
operatorStack.pop();
processOperator(toProcess);
}
if (!operatorStack.empty() && operatorStack.peek() == '(') {
operatorStack.pop();
} else {
System.out.println("Error: unbalanced parenthesis.");
error = true;
}
}
}
// Empty out the operator stack at the end of the input
while (!operatorStack.empty() && isOperator(operatorStack.peek())) {
char toProcess = operatorStack.peek();
operatorStack.pop();
processOperator(toProcess);
}
// Print the result if no error has been seen.
if (error == false) {
double result = valueStack.peek();
valueStack.pop();
if (!operatorStack.empty() || !valueStack.empty()) {
System.out.println("Expression error.");
} else {
System.out.println("The result is " + result);
}
}
}
public static void main(String[] args) {
Scanner input = new Scanner(System.in);
// The original input
System.out.print("Enter an expression to compute: ");
String userInput = input.nextLine();
FullCalculator calc = new FullCalculator();
calc.processInput(userInput);
}
}
Most of the work here gets done by the processInput method, which take an input String, breaks it into individual tokens, and then processes those tokens to evaluate the expression.