Repetition with the while loop
The for loop is not the only looping construct in Python. As an alternative to the for loop you can use the while loop, which has the following structure:
while <test>: # statements to be repeated
Here is what happens when you reach a while loop:
- Evaluate the test.
- If the test is false, go on to the next statement after the body.
- If the test is true, do the <statements to be repeated>.
- Go back to step 1.
The while loop is useful in situations where we are not iterating over a list of data items and we also don't know in advance how many repetitions we will have to do.
Here is a typical example. Suppose we wanted to compute the largest power of 2 that was less than or equal to some other integer n. This logic will compute that power.
power = 1
n = int(input('Enter a positive integer n: '))
while power <= n:
power *= 2
# When we exit the loop power will be too large.
# Divide it by 2 to fix this problem.
power = power//2
print(str(power)+' is the largest power of 2 that is <= '+str(n))
Dynamic lists
Some computational processes produce an unpredictable amout of results. An example of a process with unpredictable results is an algorithm to find all of the prime factors of an integer. Before we have computed the divisors we can not predict how many factors the number may have.
In situations like this, the standard approach in Python is to make a list to hold the results, but make the list be empty initially. As we discover more results we append them to the list using the list append() method. A method in Python is a function that gets applied to an object. Each data item in a Python program is an object, and many different data types offer specialized methods that you can call on objects of that type. Methods are easy to recognize in the Python program, because they are invoked using a special 'dot' syntax that take the form
<variable>.<method name>(<optional arguments>)
Here is the code for a program that constructs a list of all of the prime factors of a given positive integer.
divisors = []
N = int(input('Enter N: '))
# 2 is the first divisor to try
d = 2
while N > 1:
if N % d == 0:
# If d divides evenly into N, add it to the list of
# divisors and divide it out of N.
divisors.append(d)
N = N//d
else:
# If d is not a divisor, move on to the next d to try.
d += 1
# Now print all the divisors we found.
for d in divisors:
print(d)
Programming Assignment
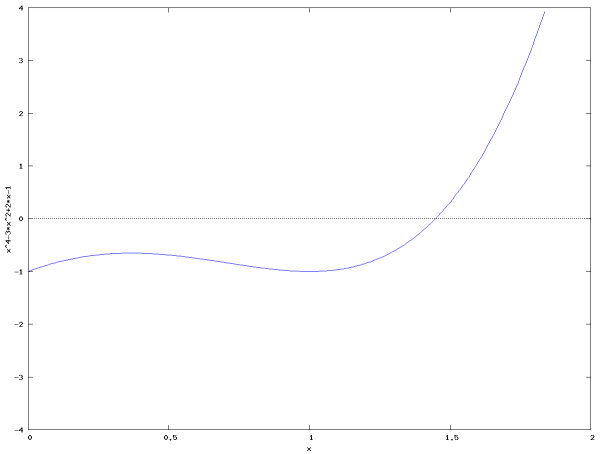
A root of a function f(x) is a value of x that causes the function to evaluate to 0. In this exercise you will construct a program that uses a simple iterative strategy to find the root of a polynomial.
The polynomial
p(x) = x4 - 3 x2 + 2 x - 1
has a root near x = 1.5, as the plot below shows.
 |
| x4 - 3 x2 + 2 x - 1 |
Note that if a = 1 and b = 2, p(a) is negative and p(b) is positive.
Here is an algorithm to find the root between a and b:
- Let c be the point on the real line that is midway between a and b.
- If p(c) and p(a) have the same sign, set a = c.
- If p(c) and p(b) have the same sign, set b = c.
- Repeat steps 1-3 until the difference between a and b is less than some threshhold you set.
Write a Python program to implement the strategy outlined above. Use a while loop to implement the algorithm, and have the while loop continue running until the difference between a and b is less than 0.0001. Have your program print the value of (a+b)/2 after the loop finishes, along with the value of the polynomial at that point.