Implementing a geometric algorithm
In these notes I am going to develop an algorithm to solve a problem in computational geometry. The problem is this: given a set of points in the plane, construct a convex polygon that just wraps around the points.
Here is an example of what we are looking for. In the picture below there are a number of points in the plane. I have wrapped a polygon around those points that just manages to enclose all of them. Note that the polygon is also a convex polygon, which means that any line segment that connects any two points on the perimeter stays entirely in the polygon.
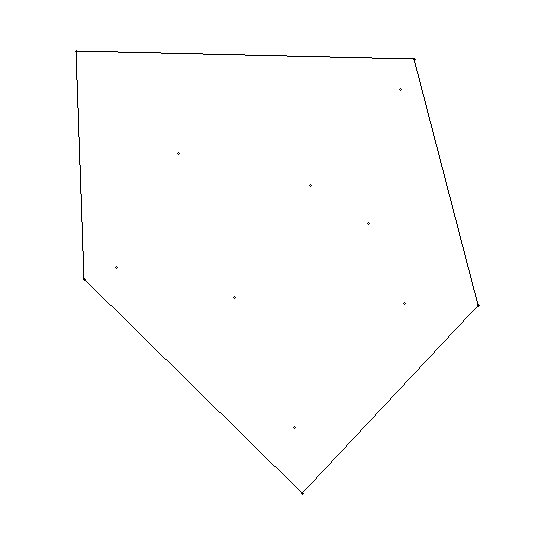
A fundamental operation
The algorithm I will present below will make use of a special operation, the "cross product" of two vectors. If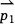 
is a vector with components x1 and y1 and 
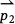is a vector with components x2 and y2 we have
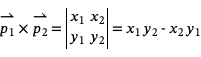
I put the word "cross product" in quotes, because this operation is not the cross product operation that you may have encountered in vector calculus. That cross product applies only to vectors in three dimensions, not to vectors in two dimensions. The "cross product" that we will be working with here is what you would get if you took a pair of two-d vectors, turned them into three-d vectors by adding a z coordinate with the value of 0, then took the regular cross product of those two vectors, and then returned the z coordinate of that cross product.
The importance of this "cross product" operation is that it gives us useful information about how to two-d vectors are oriented relative to each other. Any vector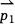 
in the plane divides the plane into two halves:
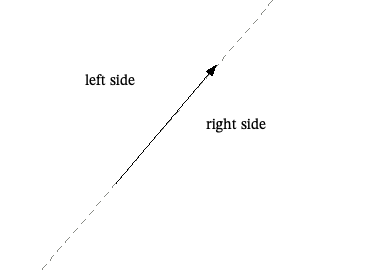
Any other vector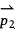 
in the plane will run in the same direction as 
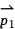, or it will lie on the left or right side of 
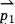. If 
× 
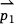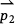is positive, then vector 
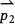lies to the left of 
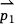. If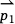 
× 
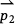is negative, then vector 
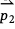lies to the right of 
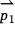. If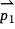 
× 
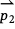is 0, then the two vectors lie in the same direction.
Since pairs of points determine vectors, we can also use this operation to answer questions about the relative orientation of points and line segments. Consider a set of three points in the plane. Points p0 and p1 together determine a line segment. Suppose we wanted to determine which side of that line segment a third point, p2 lies on. This is something we could use the cross product for. The first step is to form a pair of vectors: the vector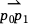 
is a vector that runs in the direction of the line segment that has points p0 and p1 as its endpoints, and the vector 
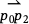runs in the direction from p0 to p2. The cross product of those two vectors can tell us whether p2 lies to the left or the right of the line segment. If the cross product is positive, p2 lies to the left of the line segment. If the cross product is negative, p2 lies to the right of the line segment.
Polar angle
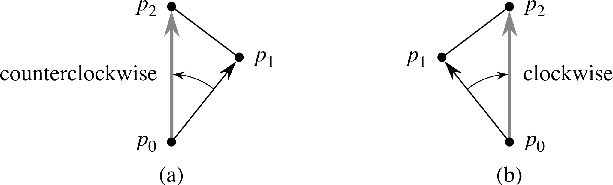
Another core operation we are going to use below is the polar angle of a point relative to a reference point. The picture below shows a point p in the plane.
The reference point in this picture is the origin. The polar angle, θ, of this point relative to the origin can be computed via the formula.
θ = arccos(x/|p|)
The problem with this formula is that it only works for points that are located above the x axis. A more useful formula for computing the polar angle is to use the atan2 function, which is defined by
Graham Scan
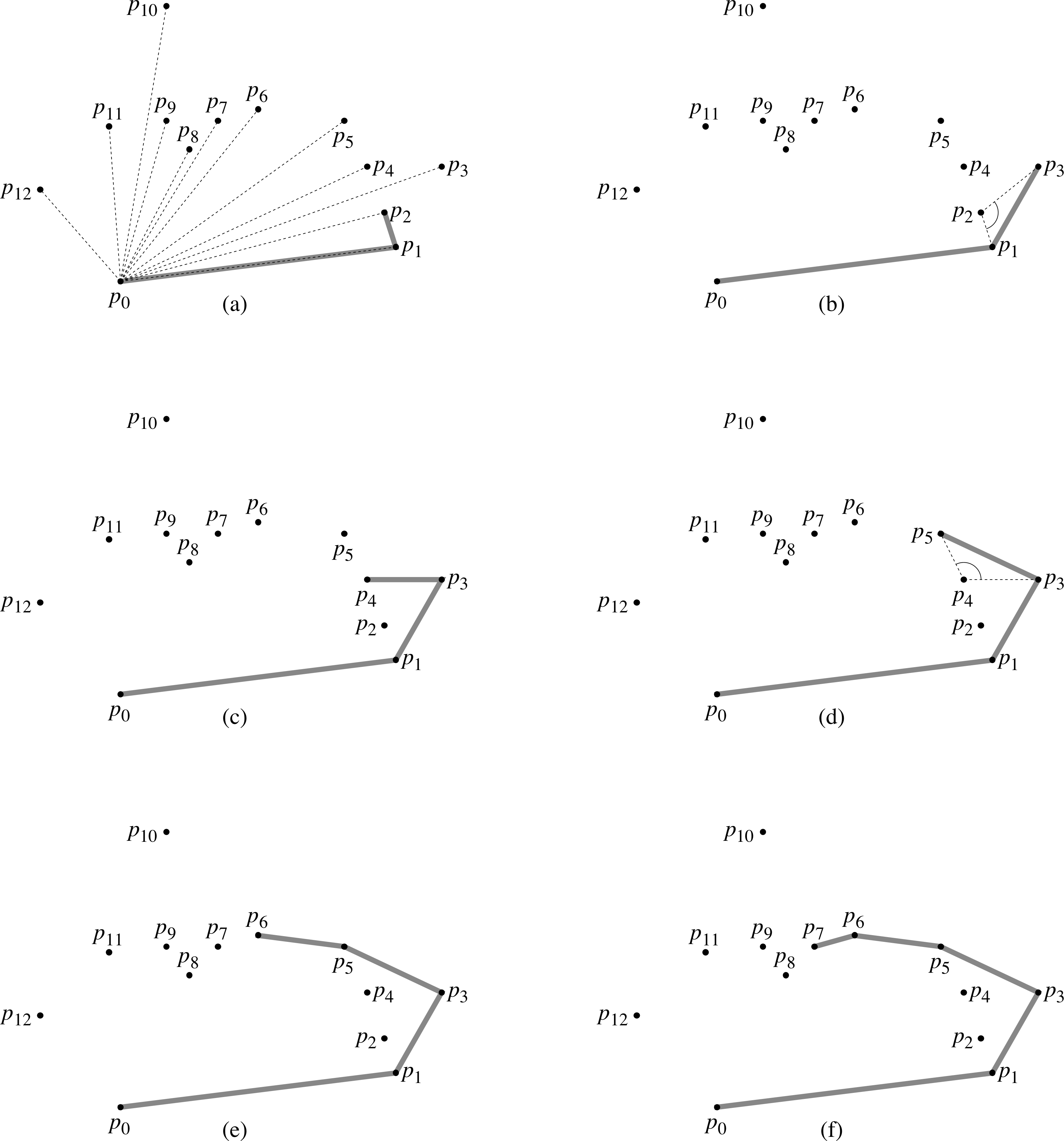
The convex hull of a set of points Q in the plane is a convex polygon that just encloses all of the points. Given a set of points in the plane, the convex hull is a curve that joins a subset of those points together. Here is an outline of an algorithm to solve this problem, the Graham scan algorithm.
GRAHAM-SCAN(Q)
let p0 be the point in Q with the minimum y-coordinate and minimum x-coordinate
let <p1,p2,…,pn> be the remaining points in Q sorted by polar angle in
counter-clockwise order around p0. If more than one point has the same
polar angle, remove all but the farthest from p0
let S be an empty stack
PUSH(p0,S)
PUSH(p1,S)
PUSH(p2,S)
for i = 3 to m
while the angle formed by the points NEXT-TO-TOP(S), TOP(S), and pi makes a nonleft turn
POP(S)
PUSH(pi,S)
return S
A key step in this algorithm is determining whether a set of three points forms a left turn or a right turn. This is a case where the "cross product" we defined above is useful. Given a set of three points, p1, p2, and p3, we form the first pair of points into a line segment. Using the procedure described in the section above, we then use the "cross product" to determine whether p3 lies on the left side or the right side of that line segment. If p3 lies on the left, these three points form a left hand turn. If p3 lies on the right, these three points form a right hand turn.
Here is a series of pictures to illustrate the operation of this algorithm in a typical example.
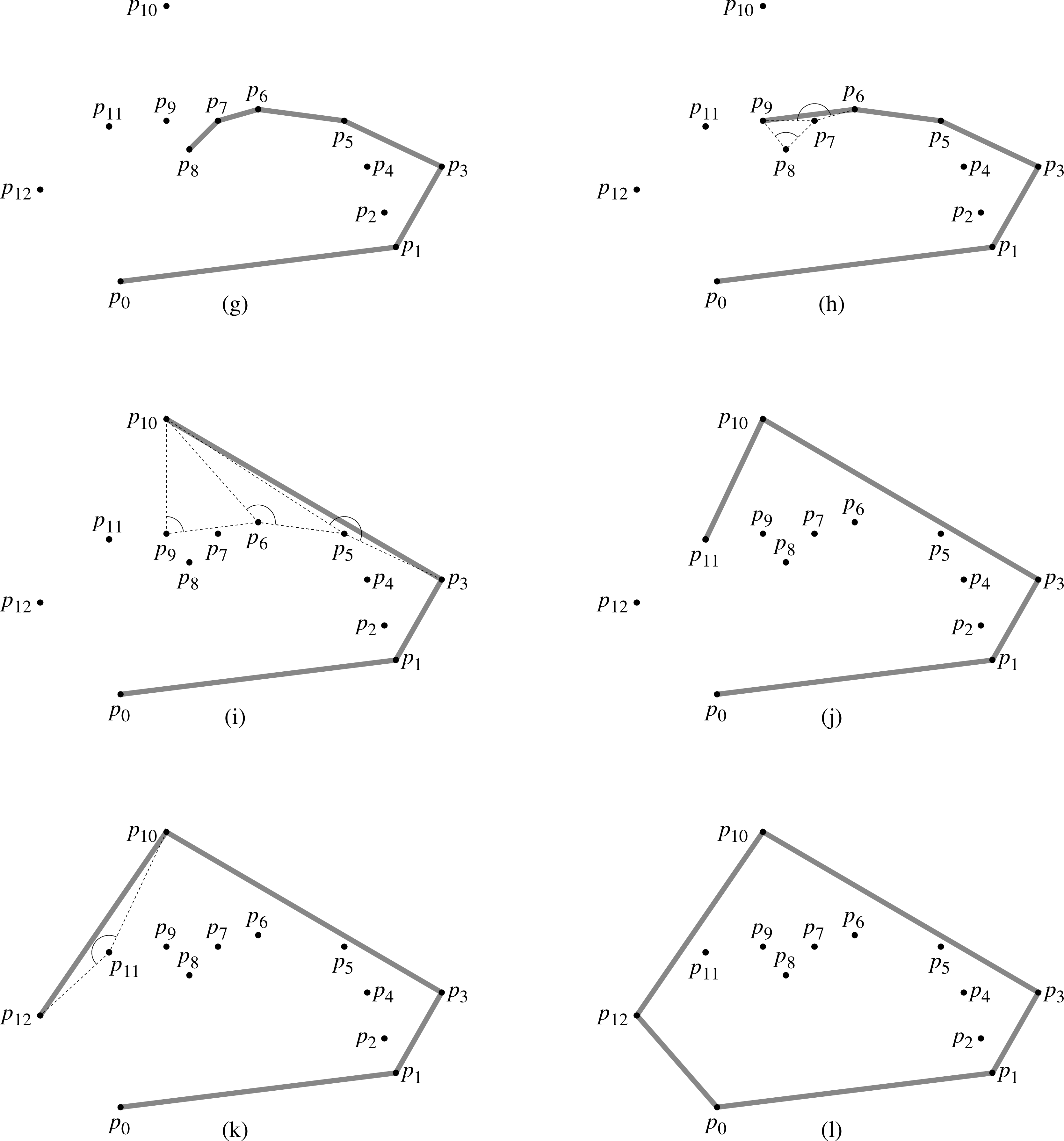
Implementation in Java
To implement this algorithm in Java we begin by setting up a couple of useful helper classes. The first of these is a simple class to represent a point in the plane.
package convexhull;
public class Point {
private float x;
private float y;
public Point(float x,float y) {
this.x = x;
this.y = y;
}
public float getX() { return x; }
public float getY() { return y; }
public void print() {
System.out.println("("+x+","+y+")");
}
}
The second is a Vector class that offers useful polarAngle() and crossProduct() methods.
package convexhull;
public class Vector {
private float x;
private float y;
public Vector(Point from,Point to) {
this.x = to.getX() - from.getX();
this.y = to.getY() - from.getY();
}
public float polarAngle() {
return (float) Math.atan2(y, x);
}
public static float crossProduct(Vector v0,Vector v1) {
return v0.x*v1.y - v1.x*v0.y;
}
}
Now we are ready to implement the algorithm.
We start with some code to load the points from a text file.
List<Point> points = new ArrayList<Point>();
Scanner input;
try {
input = new Scanner(new File("points.txt"));
} catch (Exception ex) {
ex.printStackTrace();
return;
}
while(input.hasNextFloat()) {
float x = input.nextFloat();
float y = input.nextFloat();
Point p = new Point(x,y);
points.add(p);
}
input.close();
The first step in the algorithm says to find the point with the smallest y coordinate. In case of ties we will select the point with the smallest y coordinate and smallest x coordinate. To implement this first step I am going to sort the points list in order of y coordinate and x coordinate. The ArrayList class has a sort() method, but it requires a little bit of help. To be able to sort a list of objects the sort() method needs to be able to compare pairs of objects to determine whether or not they are in the correct order. Since the sort() method does not know how to do this comparison it is going to ask us to provide a method that takes two objects as its parameters and then returns a negative number if the first object comes before the second in the order we want, 0 if the two objects are the same, and a positive number if the first object comes after the second in the order we want. Unfortunately, Java does not offer a way to pass a method to another method, so we have to instead put the method we want to pass to sort() inside an object and then pass that object to sort(). This in turn causes another problem: how will sort() know which method in the object to call? The solution to this problem is to use an interface. The Java class library defines a Comparator interface that contains a compare() method for us to implement.
To sort our list of points in the order we want we define the following class that implements the Compartor interface and provides a version of the compare() method:
class CompareXY implements Comparator<Point> {
@Override
public int compare(Point o1, Point o2) {
if(o1.getY() < o2.getY()) {
return -1;
} else if(o1.getY() > o2.getY()) {
return 1;
} else if(o1.getX() < o2.getX()) {
return -1;
} else if(o1.getX() > o2.getX()) {
return 1;
}
return 0;
}
}
We are now in a position to sort our list of points. After sorting we pull out the point with the smallest y and x values.
points.sort(new CompareXY()); Point p0 = points.get(0); points.remove(0);
The next step in the algorithm is to sort the remaining points by their polar relative to the p0 point. To do this we introduce another comparator class
class CompareAngle implements Comparator<Point> {
private Point p0;
public CompareAngle(Point p) {
p0 = p;
}
@Override
public int compare(Point o1, Point o2) {
Vector v1 = new Vector(p0,o1);
Vector v2 = new Vector(p0,o2);
float angle1 = v1.polarAngle();
float angle2 = v2.polarAngle();
if(angle1 < angle2) {
return -1;
} else if(angle1 > angle2) {
return 1;
}
return 0;
}
}
and then we can sort our remaining points by polar angle.
points.sort(new CompareAngle(p0));
Next we need to set up a stack and push three points onto it. Fortunately, the Java class library has a Stack class that we can use.
Stack<Point> s = new Stack<Point>(); s.push(p0); s.push(points.get(0)); s.push(points.get(1));
We are now ready for the main loop in the algorithm. One of the things we will need to do in the body of the main loop is to judge whether a sequence of three points forms a left hand turn or a right hand turn. I have written a helper function to make that determination.
public static boolean isRightTurn(Point p0,Point p1,Point p2) {
Vector v0 = new Vector(p0,p1);
Vector v1 = new Vector(p0,p2);
return Vector.crossProduct(v0,v1) < 0.0f;
}
Here now is the code for the main loop of the algorithm.
for(int n = 2;n < points.size();n++) {
Point next = points.get(n);
Point top = s.peek();
s.pop();
Point nextToTop = s.peek();
s.push(top);
while(isRightTurn(nextToTop,top,next)) {
s.pop();
top = s.peek();
s.pop();
nextToTop = s.peek();
s.push(top);
}
s.push(next);
}
At the conclusion of this loop the points that make up the boundary will be stored in the stack. All we have to do is to iterate over the points in the stack and print them out.
for(Point p : s) {
p.print();
}