Lagrange Interpolation

Polynomial Interpolation

The polynomial interpolation problem is the problem of constructing a polynomial that passes through or interpolates n+1 data points (x₀, y₀), (x₁, y₁), ... , (x_n, y_n).

Lagrange Interpolation

In 1795 the French mathematician Joseph-Louis Lagrange published an algorithm for constructing an interpolating polynomial from a set of data points.

To construct a polynomial of degree n passing through n+1 data points (x₀, y₀), (x₁, y₁), ... , (x_n, y_n) we start by constructing a set of basis polynomials L_n,k(x) with the property that

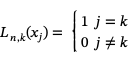
These basis polynomials are easy to construct. For example for a sequence of x values {x₀, x₁, x₂, x₃} we would have the four basis polynomials

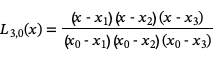
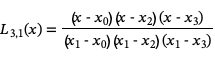
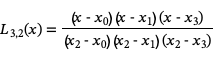
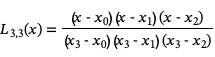
Once we have constructed these basis functions, we can form the n^th degree Lagrange interpolating polynomial

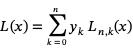
This polynomial does what we want it to do, because when x = x_j every one of the basis functions vanishes, except for L_n,j(x), which has value 1. Thus L(x_j) = y_j for every j and the polynomial interpolates each one of the data points in the original data set.

Since an n^th degree polynomial is uniquely determined by its value at n+1 points, this is the unique polynomial passing through the data points.

An example

Here is a set of data points.

x	y
4.1168	0.213631
4.19236	0.214232
4.20967	0.21441
4.46908	0.218788

Here is a plot of these points showing that they line up along a curve, but the curve is not quite linear.

x y

4.116799999999999 0.213630999999999

4.192359999999999 0.214232000000000

4.20967 0.214409999999999

4.469079999999999 0.218788000000000

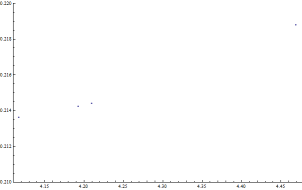To construct the Lagrange interpolating polynomial of degree 3 passing through these points we first compute basis functions:

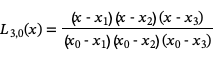
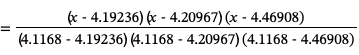
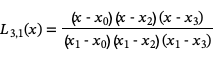
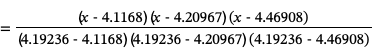
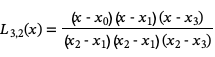
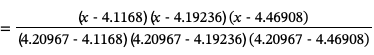
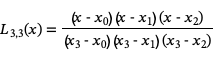
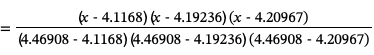
From these we construct the interpolating polynomial:

L(x) = y₀ L_3,0(x) + y₁ L_3,1(x) + y₂ L_3,2(x) + y₃ L_3,3(x)

= -0.00355245 x³ + 0.0695519 x² - 0.386008 x + 0.871839

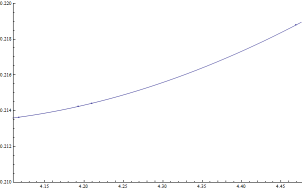
Here are the original data points plotted along with the interpolating polynomial.

x y

4.116799999999998 0.213630999999998

4.192359999999999 0.214232000000000

4.20967 0.214409999999998

4.469079999999999 0.218788000000000

y = -0.00355245 x³ + 0.0695519 x² - 0.386008 x + 0.871839

A program to compute Lagrange polynomials

Our next example program is a program to construct and evaluate a Lagrange polynomial from a set of data points. I will be using this this program as an opportunity to show more examples of classes, and to demonstrate how we can use classes to decompose a complex problem into smaller simpler parts.

Once we have constructed a program that can read a set of data points and construct an interpolating polynomial from them we will use the interpolating polynomial to solve a problem.

A class to represent a data point

Lagrange interpolating polynomials are constructed from a list of data points, where each data point is a combination of an x value and a y value.

Here is the code for a simple class we can use to represent our data points.

package interpolation;

public class DataPoint {
    private float x;
    private float y;
    
    public DataPoint(float x,float y) {
        this.x = x;
        this.y = y;
    }
    
    public float getX() { return x; }
    public float getY() { return y; }
}

A class to represent a data set

Data points get organized into data sets. A data set is simply a list of data points.

Here is a class I have constructed to help us model a data set:

package interpolation;

import java.util.ArrayList;
import java.util.List;
import java.util.Scanner;

public class PointSet {
    private List<DataPoint> points;
    
    public PointSet() {
        points = new ArrayList<DataPoint>();
    }
    
    public void readFrom(Scanner input) {
        while(input.hasNextFloat()) {
            float x = input.nextFloat();
            float y = input.nextFloat();
            points.add(new DataPoint(x,y));
        }
    }
    
    public List<Float> getXs() {
        ArrayList<Float> result = new ArrayList<Float>();
        for(DataPoint dp : points) {
            result.add(dp.getX());
        }
        return result;
    }
    
    public List<Float> getYs() {
        ArrayList<Float> result = new ArrayList<Float>();
        for(DataPoint dp : points) {
            result.add(dp.getY());
        }
        return result;
    }
}

Since we are going to be reading our data sets from a text file, I have provided a member function here to read those data points from a text file.

The Lagrange interpolation algorithm I showed earlier makes heavy use of lists of x values and lists of y values. To help us generate those lists from a data set I have also provided methods getXs() and getYs() that return a list of x values and a list of y values, respectively.

A class to represent a Lagrange polynomial

The next class we are going to work with is a class that represents a Lagrange polynomial that we have constructed from a set of data points. Here is the code for that class.

package interpolation;

import java.util.ArrayList;
import java.util.List;

public class LagrangePoly {
    private List<Float> ys;
    private List<BasisFunction> ls;
    
    public LagrangePoly(PointSet data) {
        ys = data.getYs();
        List<Float> xs = data.getXs();
        ls = new ArrayList<BasisFunction>();
        for(int k = 0;k < xs.size();k++) {
            ls.add(new BasisFunction(xs,k));
        }
    }
    
    public float evalAt(float x) {
        float sum = 0.0f;
        for(int k = 0;k < ys.size();k++) {
            sum += ys.get(k)*ls.get(k).evalAt(x);
        }
        return sum;
    }
}

Note that the constructor for this class takes a PointSet object as its parameter. From that set of data points the class will then construct the list of basis functions and y values that the polynomial is composed of.

Since we are constructing a polynomial, we will eventually want to evaluate that polynomial at some x values. To make that possible I have provided an evalAt() method that evaluates the polynomial at a given x value and returns the value of the polynomial at that x.

A problem to solve

In the project I have provided you will also find a text file named population.txt. That text file contains population data from the US census from 1960 to 2010. We are going to construct an interpolating polynomial from that data and use it to estimate the US population in the year 1985.

I have also provided you with one last class that contains the main method you will use to solve this problem:

package interpolation;

import java.io.File;
import java.util.Scanner;

public class Interpolation {

    public static void main(String[] args) {
       Scanner input;
       try { 
           input = new Scanner(new File("population.txt"));
       } catch(Exception ex) {
           ex.printStackTrace();
           return;
       }
       
       PointSet points = new PointSet();
       points.readFrom(input);
       input.close();
       
       LagrangePoly p = new LagrangePoly(points);
       
       input = new Scanner(System.in);
       System.out.print("Enter a year: ");
       int year = input.nextInt();
       System.out.println("The approximate population of the US in " + year + " is " + (int) p.evalAt(year));
    }
    
}

A missing class

I have intentionally left one class out of my program. Your job will be to write the code for the missing BasisFunction class. From the code I have provided you can see what form the constructor for that class will take, and you can also see that the class needs to have an evalAt() method that will allow you to evaluate that basis function at a given x value.

Here is a helpful hint: from the discussion above you can see that a basis function is a fraction whose numerator depends on an x value and the x values of the data points and a denominator that depends only on the x values of the data points. This means that you can compute that denominator ahead of time and store it in a member variable. That way the evalAt() method will only need to compute the numerator and then divide that by the precomputed denominator.