Another alternative

In this programming exercise we are going to construct a third version of the difference finding algorithm, along with a third version of a strategy for generating the two files of random integers.

First off, here is an alternative algorithm for generating a file of random numbers with no repeats similar to the files we generated in versions one and two:

1. Fill an array of size N with the numbers 0..(N-1)
2. Shuffle the array
3. Write the first N (1-1/e) ≈ 0.6321206 N numbers in the shuffled array out to the file.

Where the does the magic number N (1-1/e) come from? For this we need a little probability theory. The probability that any given number will appear at least once when we select N numbers at random from the range 0..N-1 is

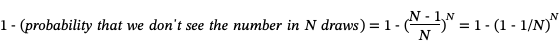
In the limit where N gets large, this is 1 - 1/e. The expected total number of distinct numbers that appear in a sequence of N draws from 0..N-1 is then just N times this 1 - 1/e factor.

Secondly, here is an algorithm to determine the list of numbers that appear in exactly one of the two files:

1. Construct an array of size N that is filled with 0s.
2. For each of the two files do this:
1. For each number n that you read from the file go to position n in the list and increment the number you find there by 1.
3. Scan through each position n in the list. If you find a 1 in that position, write the number n out to the output file.

How to turn in your work

To submit your work for grading, compress your project folder into a zip archive and upload that archive to the course Canvas page.