Drawing the Teapot
In this exercise we will draw the famous Utah teapot.

Start by downloading the starter code I have provided. This starter code is a modified version of program 12.2 from the text. That program draws a single Bezier patch and applies a texture to it.
In main.cpp you will see the control grid for this single Bezier patch being set up in the setupVertices() function.
Replace the code that sets up the control grid for the patch with code that instead reads a list of several control grids from the text file Teapot.txt. This file contains the complete control grid data for the Utah teapot. The teapot is made up of 32 Bezier patches. You will also need to replace
glDrawArrays(GL_PATCHES, 0, 16);
in the display() function with
glDrawArrays(GL_PATCHES, 0, 16*32);
since we are now drawing 32 patches instead of one.
Drawing a wireframe
To confirm that you have correctly loaded the control points, draw the teapot first in wireframe mode.
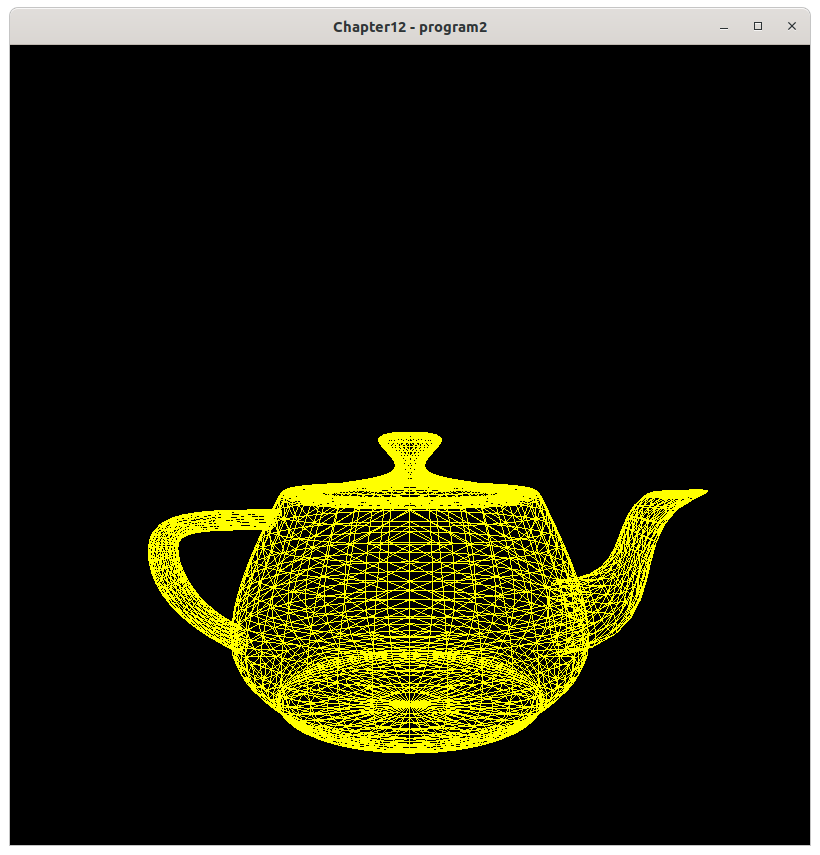
To do this, replace the line
glPolygonMode(GL_FRONT_AND_BACK, GL_FILL);
with
glPolygonMode(GL_FRONT_AND_BACK, GL_LINE);
and use this simple fragment shader program:
#version 430
out vec4 color;
void main(void)
{
color = vec4(1.0, 1.0, 0.0, 1.0);
}
You will also need to apply a transformation to orient the teapot correctly.
Applying a lighting model
Modify the code I provided so that it no longer uses a texture to color the patch. Instead, apply a material color to the teapot and light it with a moving light and the same lighting model you used for assignment three.
To use the lighting model you will need to compute normals for each point in your Bezier patch. Here is how to do that.
Points on the surface of a Bezier patch are computed via the formula
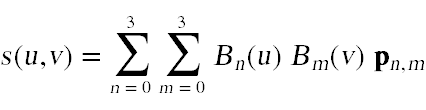
where the Bernstein polynomials are
B0(u) = (1 - u)3
B1(u) = 3 u (1 - u)2
B2(u) = 3 u2 (1 - u)
B3(u) = u3
To compute a normal at each point on Bezier patch we start by computing a couple of tangent vectors:
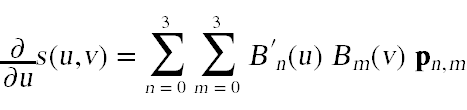
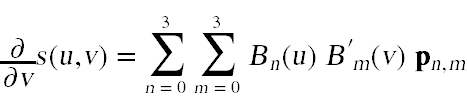
where
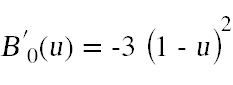
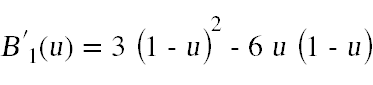
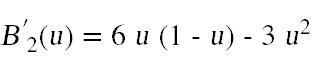
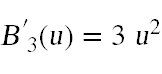
are the derivatives of the Bernstein polynomials. To compute the normal at the point s(u,v), normalize these two vectors and take their cross product. The normal calculations can be done in the tessellation evaluation shader along with the computation of the output points. Don't forget that the normals will need to be transformed before returning them. You can examine the code for assignment three to see how to correctly transform normals.
To get the teapot to draw correctly, also don't forget to turn on depth testing:
glEnable(GL_DEPTH_TEST); glDepthFunc(GL_LEQUAL);