CFGs and PDAs are equivalent

Theorem A language L is generated by a CFG if and only some PDA accepts L.

Proof Since this is an if and only if theorem we have to prove it in both directions. I will present this as two separate proofs.

First half

Theorem If some PDA accepts a language L, there exists a context-free grammar that generates L.

Proof To start with, we standardize the PDA:

1. Add a new symbol # to the stack alphabet.
2. Create a new start state for the PDA and add this transition from the new start state to the old start state.



3. If the original PDA accepts some inputs without emptying its stack, modify the accepting states to empty out the stack.
4. If the PDA has more than one accepting state, turn all of the accepting states into regular states and add a transition that looks like the following to connect the former accepting state to the new accepting state.



5. If any transition in the PDA both pops a symbol and pushes a symbol on the same transition (such as a,b→c), replace it with

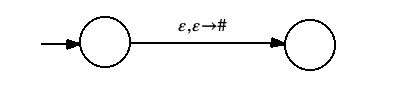
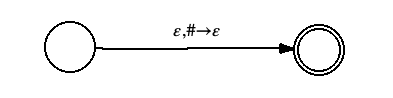
Now, assuming that the start state of the PDA is s and the sole accepting state is f, we create a collection of grammar rules:

S →A_s,f

A_p,p → ε

A_p,q → A_p,r A_r,q

The latter rules are created for all possible triples (p,r,q) in Q×Q×Q.

Finally, for every pair of states p and q that have transitions looking like

add a grammar rule

A_p,q →a A_r,t b

Now, let x be any string accepted by the PDA. We argue that the grammar we have just created can generate x. To do this, we prove something more general:

Lemma x can take the PDA from state p with an empty stack to state q with an empty stack if and only if A_p,q generates x.

Proof part one

If x can take the PDA from state p with an empty stack to state q with an empty stack then A_p,q generates x

Proof is by induction on the number of transitions on the path from p to q.

Base case: If the path from p to q has length 0, the PDA has no opportunity to read any input symbols. Thus x = ε, and also p = q. The grammar rule A_p,p → ε generates x.

Induction step: suppose the path from p to q has n steps. If the symbol pushed in the first step on the path is the same as the symbol popped on the last step and x takes the form ayb, then the first rule in the derivation of x will be A_p,q →a A_r,t b. The path from r to t takes n-2 steps, so by the induction hypothesis A_r,t can generate y, and we have A_p,q →a A_r,t b ⇒ a y b = x

If the first symbol pushed on the path from p to q is not the same as the last symbol popped, there will have to be a state r on that path where the first symbol pushed gets popped off again. In that case, the step A_p,q → A_p,r A_r,q is the first step in the derivation of x = yz. Since the paths from p to r and from r to q are shorter than the path from p to q, the induction hypothesis gives us that A_p,r derives y and A_r,q derives z, and we have A_p,q → A_p,r A_r,q ⇒ y A_r,q ⇒ y z = x.

Proof part two

If A_p,q generates x, then x can take the PDA from state p with an empty stack to state q with an empty stack.

Proof is by induction on the number of steps in the derivation of x.

Base case: If the derivation of x contains only one step, then that step must take the form A_p,p → ε. In this case p = q and x = ε. There is certainly a path in the machine that goes from state p to state p and reads nothing.

Induction step: Consider the first step in the derivation of x from A_p,q. There are two possibilities for what this first step is.

If it takes the form A_p,q → A_p,r A_r,q we let y be the string derived from A_p,r and we let z be the string derived from A_r,q. Both of these subderivations have fewer steps than the derivation of x, so the induction hypothesis allows us to say that y takes the machine from state p with an empty stack to state r with an empty stack, and that z takes the machine from state r with an empty stack to state q with an empty stack. Thus, x = yz takes the machine from state p with an empty stack to state q with an empty stack.

If the first step in the derivation takes the form A_p,q →a A_r,t b we see that the machine can start by reading a and pushing something on the stack and then later read b while popping that same thing from the stack. This tells us that x = a y b. Also, we see that A_r,t derives y. Since that derivation is necessarily shorter than the derivation of x, the induction hypothesis allows us to say that the machine can take us from state r with an empty stack to state t with an empty stack. Putting this all together, we now see that x takes us from state p with an empty stack to state q with an empty stack.

Second half

Theorem If L is a CFL, there exists a PDA that accepts L.

Proof The picture below shows the structure of the PDA:

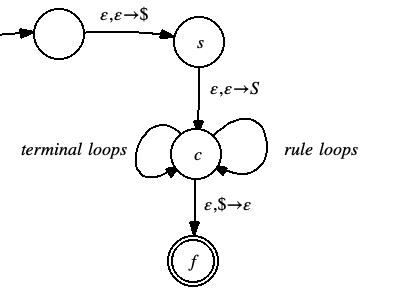
The rule loops are a collection of loops, one for each grammar rule. For example, if the grammar contains a rule

A → x B C

the machine will contain a loop that looks like this:

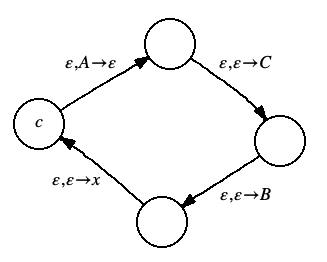
The loop pops an A from the stack and then pushes the items in the rule's right hand side onto the stack in reverse order. The ensures that the first item on the right hand side ends up at the top of the stack and is available for the next operation.

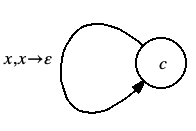
The terminal loops match a terminal sitting at the top of the stack with that same terminal coming in from the input.

The machine works by guessing derivations of input strings. If the machine is able to guess the proper derivation and eventually match every character of the input by using terminal loops, the machine can arrive at the final state with an empty stack.