A machine that prints its own description

Let P_x be the following Turing machine:

On input w:

1. Erase the tape.
2. Print x on the tape, then halt.

Now consider the machine B, which is essentially a P_x builder.

On input w:

1. Construct P_w.
2. Erase the tape.
3. Write <P_w> on the tape, followed by w, then halt.

Next, we consider machines that are compositions of other Turing machines. For example, suppose N and M are Turing machines. The composition NM is the machine that does the following.

On input w:

1. Run N on the input until N halts.
2. Rewind the tape head to the start of the tape.
3. Run M on whatever N left on the tape.

Using the machines and ideas defined above, we can now construct a machine that prints its own description. The machine is the composition P_<B>B. Here is what the machine does:

1. Erase the tape.
2. Print <B> on the tape.
3. Construct P_<B>, then print <P_<B>> on the tape followed by <B>.

The recursion theorem

The recursion theorem establishes establishes introspection as a valid technique for Turing machines to use. In the introspection technique a Turing machine obtains its own description and then uses that description as part of the computation it is doing.

Here is the formal statement of the recursion theorem.

Theorem Let T be a Turing machine that computes a function t: Σ^*×Σ^*→Σ^*. There is a Turing machine R that computes a function r: Σ^*→Σ^* such that

r(w) = t(<R>,w)

for all w ∈ Σ^*.

One way to prove the recursion theorem is by construction. We demonstrate how to convert any Turing machine T into the new machine R described in the theorem.

The machine we need is a composition: P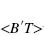BT. The first part of the machine is a slightly modified version of P_x:

On input w:

1. Erase the tape.
2. Print x on the tape, followed by w, then halt.

Likewise, B is a slightly modified version of B:

On input x,w:

1. Construct P_x.
2. Erase the tape.
3. Print <P_x> on the tape, followed by x and then w.
4. Halt.

The following sequence shows what the tape looks like when we run R =P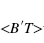BT on any input w:

At start: w
After P runs: <BT>,w
After B runs: <PBT>,w
After T runs: t(<PBT>,w)

We now have a machine R which when run on any input w computes t(<R>,w).

Applications of the recursion theorem

As I mentioned above, the primary new capability that the recursion theorem provides is the capability of introspection. This means that we can construct machines that appear to be able to see and use their own descriptions. Of course machines can't do this, but the recursion theorem gives us the next best thing: machines that behave as if they were able to see their own descriptions.

Here is an example of this. Suppose we wanted to use the recursion theorem to build a machine that can print itself. We start by constructing an appropriate T:

On input <M>,w:

1. Erase the tape.
2. Print <M> on the tape and halt.

This machine T implements the mapping t(<M>,w) = <M>. The recursion theorem then guarantees that there exists a machine R that computes a function r(w) = t(<R>,w) = <R>.

Here is what R does:

On input w:

1. Erase the tape.
2. Print <R> on the tape and halt.

This machine appears to be able to obtain and use its own description. It is not actually able to see itself, but it at least behaves as if it were able to. Once we have a machine that exhibits the behavior we want, we can change our terminology at tiny bit and rewrite the description of R this way.

On input w:

1. Erase the tape.
2. Obtain our own description, <R>.
3. Print <R> on the tape and halt.

One primary application of the recursion theorem is that it makes proofs of common results in the Theory of Computation easier to construct. The classic example is the proof by contradiction that A_TM is undecidable much easier to construct.

Suppose that A_TM is decidable by some machine H. We use H to construct a machine B:

On input w:

1. Obtain our own description, <B>.
2. Run H on the pair <B,w> and do the opposite of what H does.

No matter what input we hand B, B will do the opposite of what H predicts it will do when run on this input.

Another interesting application is the proof that it is impossible to determine whether or not some Turing machine T is the smallest possible Turing machine that accepts L(T). To prove this result, we introduce the language

MIN_TM = {<M> | <M> is the smallest machine that accepts L(M) }

Here is a contradiction proof that this language is undecidable. We use the recursion theorem to construct a special machine C:

On input w:

1. Obtain our own description, <C>.
2. Run the enumerator for MIN_TM until it prints a description of a machine <D> that is longer than <C>.
3. Simulate D running on w and do what it does.

The machine we just constructed accepts the same language as the larger machine D. This is a contradiction, because the set MIN_TM that D came from is supposed to consist of machines that are the smallest machine that accept their language.