Time efficiency of Turing machine programs
Up to this point in this course our main concern has been whether or not problems are decidable. In practice, there is another consideration. Some decidable languages have deciders that are very efficient. An inefficient decider will take a large number of steps to decide some of its inputs. In some cases the number of steps required is so large that the decider essentially becomes unworkable.
The next major distinction we are going to draw is the distinction between languages for which we can find efficient deciders and decidable languages that do not have an efficient decider. The first step in this process is to define what we mean by "efficient decider". The second step will be to build up a theoretical framework that allows us to prove that certain decidable languages do not have an efficient decider.
Here is our first important definition.
Definition A language L is polynomial time decidable if there exists a Turing machine M that decides the language in f(|w|) steps or fewer for every input string w, where f(x) is a polynomial function of its input.
Here also is another important, closely related definition.
Definition A language L is in the class P if there exists a polynomial time decider for L.
Some examples
In chapter four we saw several examples of Turing machine programs to decide simple languages. Many of the languages in those examples were in the class P.
For example, we saw that the language
L = { ww | w ∈ Σ* }
was decidable by a Turing machine. That Turing machine did its work by going through three stages. Here are those stages, along with the number of steps required for each stage given an input of length n:
- Make a pass across the input to confirm that the input has even length, then rewind to the start. (2 n steps)
- Make a series of passes across the tape. On each pass mark out one character on the left end and one character on the right. (A maximum 2 n steps for each pass, n/2 passes, for a total of at most n2 steps.)
- Make a series of passes across the tape. One each pass locate a character in the left half and match it with the corresponding location on the right half. (A maximum 2 n steps for each pass, n/2 passes, for a total of at most n2 steps.)
This analysis shows that the number of steps needed to decide an input w in this language as a function of n = |w| is f(n) = 2 n2 + 2 n.
There are many real-world problems in computer science that can be shown to have polynomial time solutions. The challenge in most cases is expressing the problem within the general framework of the theory of computation. Here is a typical problem. Suppose you have a directed graph, and you want to determine whether or not a path exists from one vertex s to another vertex t in the graph. This problem can be expressed as a language:
PATH = {<G,s,t> | G encodes a directed graph, s and t are vertices in G, and ∃ a path from s to t }
In section 7.2 the author constructs a Turing machine that can decide PATH in polynomial time.
On input <G,s,t>:
- Place a mark on s.
- Repeat until no more nodes can be marked:
- Scan all edges in G. If G connects a marked node u to an unmarked node v, mark v.
- If t is marked, accept. Otherwise, reject.
Most of the work in this algorithm is in step 2. To perform a scan of the edges we have to read across the description of G. The number of rounds needed in step 2 is bounded above by the number of edges, and the number of edges is bounded above by the length of the entire input. This puts an upper bound of n·n = n2 on the number of steps needed in part 2. This dominates the computation time, so the number of steps needed to decide this language is polynomial in the length of the input.
The class NP
One of the central questions in the theory of computation is determining whether or not a decidable language is in the class P. As we shall see below, there is no known algorithm for doing this. At the same time, theorists suspect that there are many decidable languages that are not in P.
Given our inability to determine whether or not a language is in P, we have to settle for a theoretical framework that has the potential for at least proving that there exist decidable languages that are not in P. The first step in setting up this framework is to introduce a class of languages that are widely thought to be the next thing beyond P.
There are two possible definitions we can give for this class of languages. Below we will show that these definitions are equivalent.
Definition A decidable language L is in the class NP if there exists a polynomial time nondeterministic Turing machine that decides L.
Definition A decidable language L is in the class NP if the language is polynomial time verifiable. A verifier for a language is a Turing machine program V which, when given a pair <w,c> where w and c are both strings, can use c to determine in polynomial time whether or not w is in L.
These definitions are equivalent.
Definition 1 ⇒ Definition 2: Suppose that a language L decidable in polynomial time by a nondeterministic Turing machine M. A verifier would take as its input a string w and a list of states that M would pass through in an accepting computation on w. The verifier simply has to confirm that when M is started with w on its tape the sequence of states given represents a valid accepting computation for M. This can be done in polynomial time.
Definition 2 ⇒ Definition 1: Suppose that a language is verifiable in polynomial time by some verifier V. Here is a description of a nondeterministic Turing machine M that can decide L:
On input w:
- Guess a certificate c.
- Simulate the pair <w,c> running on V.
- If V accepts, accept. Otherwise, reject.
Examples of languages in NP
The formula satisfiability problem is the problem of determining whether or not a Boolean formula has a satisfying assignment.
A Boolean formula is an expression made up of Boolean variables and the Boolean logic operators ∧, ∨, and ¬. The formula is satifiable if there exists a set of true, false assignments for the variables that causes the entire expression to evaluate to true. Here is an example. The formula
(¬ x ∧ y) ∨ (x ∧ ¬ z)
is satisfiable via the assignments x = F, y = T, z = F.
This problem can be expressed as a language
SAT = { φ | φ is a Boolean formula with a satisfying assignment }
A verifier for SAT would take as its input a formula φ along with a list of true, false values for the variables in φ. The verifier can verify in polynomial time that when we substitute the true, false values given into the variables the formula evaluates to true.
In graph theory, a clique of size k in an undirected graph G is a set of k vertices in the graph such that every vertex in the set is connected to every other vertex in the set. This can be expressed as a language:
CLIQUE = { <G,k> | G is a graph containing a clique of size k }
A verifier for this language would take as its input a pair <G,k> and a list of the vertices in a clique of size k. The verifier simply has to confirm that each of the vertices in the given list is connected to all of the other vertices in the list.
P ≠ NP
The most famous conjecture in the theory of computation is the conjecture that P and NP represent distinct classes of languages. To prove this conjecture we would have to come up with a language in NP and then prove that it does not have a polynomial time decider. Unfortuntately, no one has been able to produce such a proof, making this a very important unproven conjecture.
The rest of these notes lay out some other definitions and results related to this conjecture.
Mapping reductions
Definition A function f(x) is a computable function if there exists some Turing machine, which, when started with x on its tape, stops running with f(x) written on its tape.
Definition A language A is mapping reducible to a language B (written A ≤m B) if there exists some computable function f such that x ∈ A if and only if f(x) ∈ B.
Here are a pair of closely related definitions, setting up the relation of polynomial time reducibility.
Definition A function f(x) is a polynomial time computable function if there exists some Turing machine, which, when started with x on its tape, stops running with f(x) written on its tape. The machine finishes its computation in a number of steps which is bounded by some polynomial function of the length of x.
Definition A language A is polynomial time reducible to a language B (written A ≤P B) if there exists some polynomial time computable function f such that x ∈ A if and only if f(x) ∈ B.
Here is one of the basic results connected to the definition of polynomial time reduction.
Theorem If A and B are Turing decidable languages with B in P and A ≤P B, then A is in P.
Proof Let f be a polynomial time computable function that maps A to B. Here is a polynomial time decider for A.
On input x:
- Compute y = f(x).
- Run the decider for B on y and accept if it does.
Clearly, this is a decider for A. If we start with an input w that is in A, f(w) will be in B, and the decider for B will accept it. Likewise, if we start with an input w that is not in A, f(w) will not be in B, and the decider for B will reject it. Since part 1 is implemented by a computable function and part 2 involves the use of a decider, none of the steps will run forever.
To prove that this is a polynomial time decider we have to give a tighter estimate on the number of steps needed to run parts 1 and 2 as a function of n = |x|. Since the mapping f is a polynomial time reduction, part 1 will take time p(n), where p is some polynomial. Because B is polynomial time decidable, part 2 will take time q(|y|), where q is some polynomial. Finally, we note that |y| ≤ p(n), because the machine that we run in part 1 can write at most one symbol on the tape for each step it takes. This shows that part 2 will take time bounded by q(|y|) ≤ q(p(n)). Since the composition of two polynomial functions p and q is also a polynomial, part 2 has a run time bounded by some polynomial function of n.
The class NPC
Because it is unknown whether or not P is the same as NP, we need some way to potentially distinguish these two classes. This motivates the introduction of yet another class, called the class of NP-complete languages, or NPC.
Definition A Turing decidable language L is NP-complete if
- L ∈ NP
- For all other languages A ∈ NP we have A ≤P L
Here is a key result related to the definition.
Theorem If A and B are both in NP, A is NP-complete, and A ≤P B, then B is NP-complete.
Proof This rests on the transitivity of the relation ≤P. Let C be any language in NP. Since A is known to be NP-complete we have
C ≤P A ≤P B
which is equivalent to
C ≤P B
Since C is any language in NP, this shows that B is NP-complete.
An initial NP-complete language
The definition of NP-completeness appears to be very difficult to satisfy. If we are going to come up with an example of an NP-complete language, the language has to capture the essense of what it means to be a language in NP.
Here is an outline of a generic strategy to map any language L in NP to a satisfiable formula:
- If a language L is in NP, there must be some NTM M that decides that language in polynomial time.
- Given a string w in the language, we can form a claim: "When we run w on M, M will reach an accepting state after running for n steps, where n ≤ p(|w|), for some polynomial function p that depends only on L and not on w."
- If we can map this claim to a logical statement expressed as a Boolean formula, we will have mapped w ∈ L to this statement. There will be a set of variable assignments that cause the statement to evaluate to true if and only if w ∈ L.
Given this, we will show to do a polynomial time reduction from any language L in NP to the language SAT. Here are some of the key details in the construction.
The construction rests on the existence of some sort of concrete proof that M accepts w. The approach we will use is to use a computation trace to provide the necessary proof. A computation trace is a record of everything the machine M does in the course of accepting an input w. The formula we will map w to is a formula that essentially says "There exists a computation trace for an accepting computation for w running on M." If w truly is in L, such a trace must exist, and the formula must be satisfiable. Conversely, if w is not in L there must be no such trace, and the formula must not be satisfiable.
A computation trace is essentially a list of configurations. Each configuration represents the state of M at some point in a computation. The configuration records what is on the tape at that stage in the computation, what state the control is in, and where the tape head is. Here is an example of a configuration. Suppose the machine is in state q, with 0x1 on the tape, and the tape head over the 1. The corresponding configuration looks like
#0xq1____________________#
The configuration simultaneously tells us where the tape head is and what state the control is in by writing the current state before the symbol on the tape that the tape head is over.
One small technical issue in constructing a configuration is to decide how many cells from the tape to show. We can determine this from the combination of w and M. Since we will know how long w is and we know the polynomial relation between the length of w and the number of steps that M will run before M decides w, we can put a bound on the number of steps for the computation. As soon as we can bound the number of steps in the computation, we can place a bound on how much stuff M could potentially write on the tape. Once we know this bound, we just need to make sure that each configuration is long enough to accomodate the maximum number of symbols that M could write in the course of the computation.
We will represent computation traces as a tableau. A tableau is a list of configurations, where each configuration follows from the previous one because there is a transition in M that allows us to go from the previous configuration to the next configuration.
Here now is the construction that builds the Boolean formula.
The variables in the Boolean formula are xi,j,s. This variable expresses the fact that cell i,j in the tableau contains character s.
The formula consists of a few large clauses, where each clause captures a key logical constraint that the tableau has to satisfy. The author calls these clauses φcell, φstart, φaccept, and φmove. Here is list of what each clause expresses.
- φcell expresses the constraint that every cell in the tableau must contain exactly one symbol.
- φstart expresses the constraint that the very first row must look like a valid starting configuration with w appearing on the tape, the tape head over the first cell, and the control for M in its start state.
- φaccept expresses the constraint that an accepting state must appear somewhere in the tableau.
- φmove captures the constraint that each row in the tableau must be the result of applying a valid transition from the previous row.
Using reductions to generate more NP-complete languages
We are now going to use the existence of the NP-complete language SAT along with the earlier theorem
Theorem If A and B are both in NP, A is NP-complete, and A ≤P B, then B is NP-complete.
to generate more examples of NP-complete languages.
The first new NP-complete language we will study is 3SAT. This is a language that is closely related to SAT. The language 3SAT consists of satisfiable Boolean formulas that take a special form. A valid formula in 3SAT can be written as the logical and of a number of clauses. Each clause must consist of exactly three terms connected by logical ors, and each term can be either a single variable or the negation of a single variable.
There is a systematic procedure in Boolean logic that can convert any arbitrary logical formula into a formula in 3SAT form. This procedure is simple enough to be done in polynomial time, so this shows that SAT is polynomial time reducible to 3SAT.
The next example shows that 3SAT is polynomial time reducible to CLIQUE.
The picture below shows how this mapping works. Given any formula in 3SAT we construct a special graph. The graph is composed of clusters of vertices, with one cluster for each clause in a formula. The vertices in clusters are connected to all of the vertices in other clusters that they are compatible with. To vertices are compatible if they use different variables or if they connect to terms with the same variables or two terms with negations of the same variables.
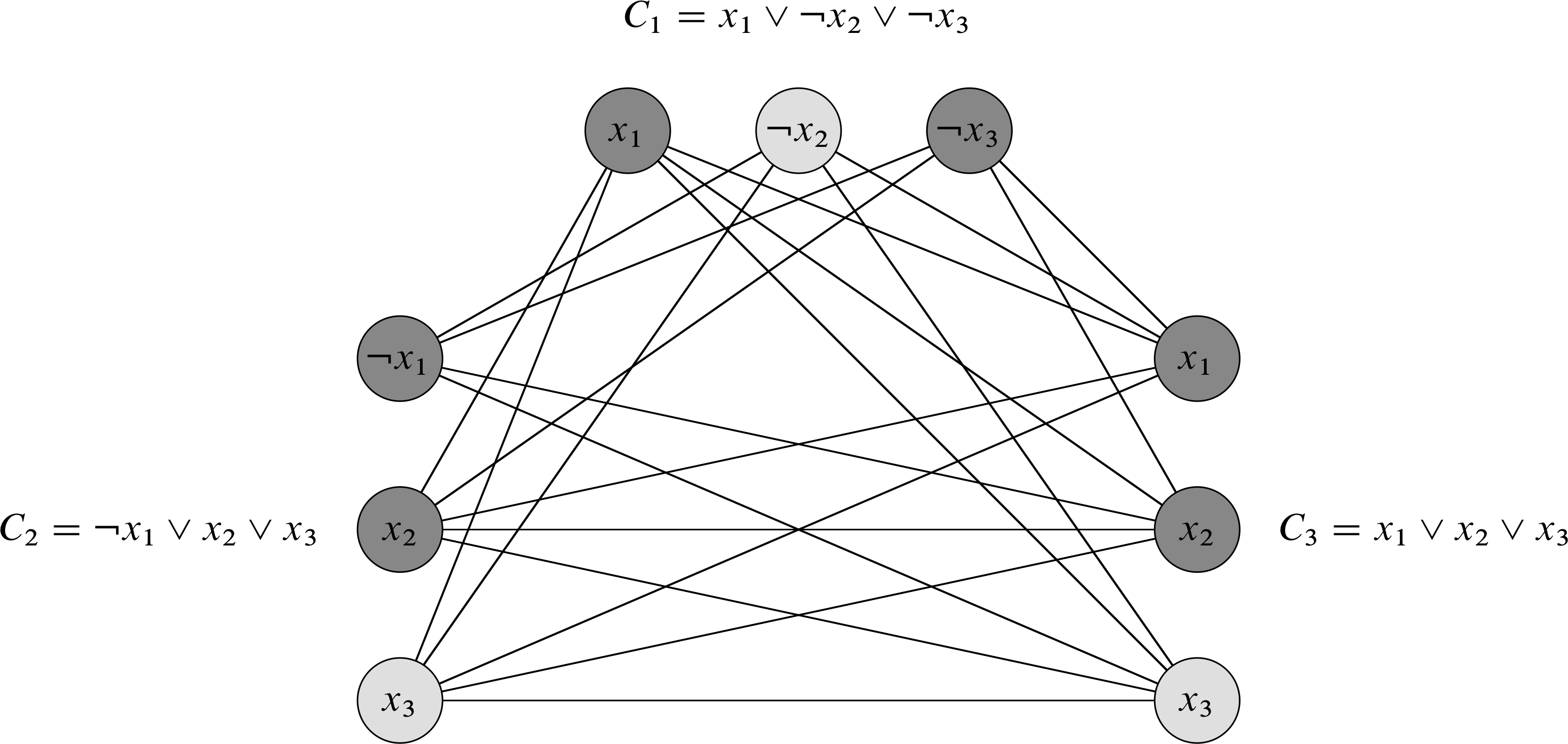
If we set k equal to the number of clauses, we see that the formula has a satisfying assignment if and only if the graph we constructed from the formula has a clique of size k. To make a satisfying assignment we must have at least one term in each clause that evaluates to true. If we select one true term in each clause the corresponding vertices in the graph must form a clique of size k because all of the vertices we have selected are compatible with each other and hence must have edges in the graph connecting them. Conversely, any clique of size k in the graph must use exactly one vertex from each group, since vertices in groups are not connected to each other. If we assign true values to terms whose vertices are in the clique we end up with a satisfying assignment for the original formula.
This mapping is sufficiently simple that we can accomplish the mapping in polynomial time.
A vertex cover in a graph is a set of vertices that cover the edges: each edge in the graph touches at least one of the vertices in the cover. This leads to a language
VERTEX-COVER = {<G,k> | G has a vertex cover of size k}
We can show that VERTEX-COVER is NP-complete via the reduction CLIQUE ≤P VERTEX-COVER.
The picture below shows how the mapping works.
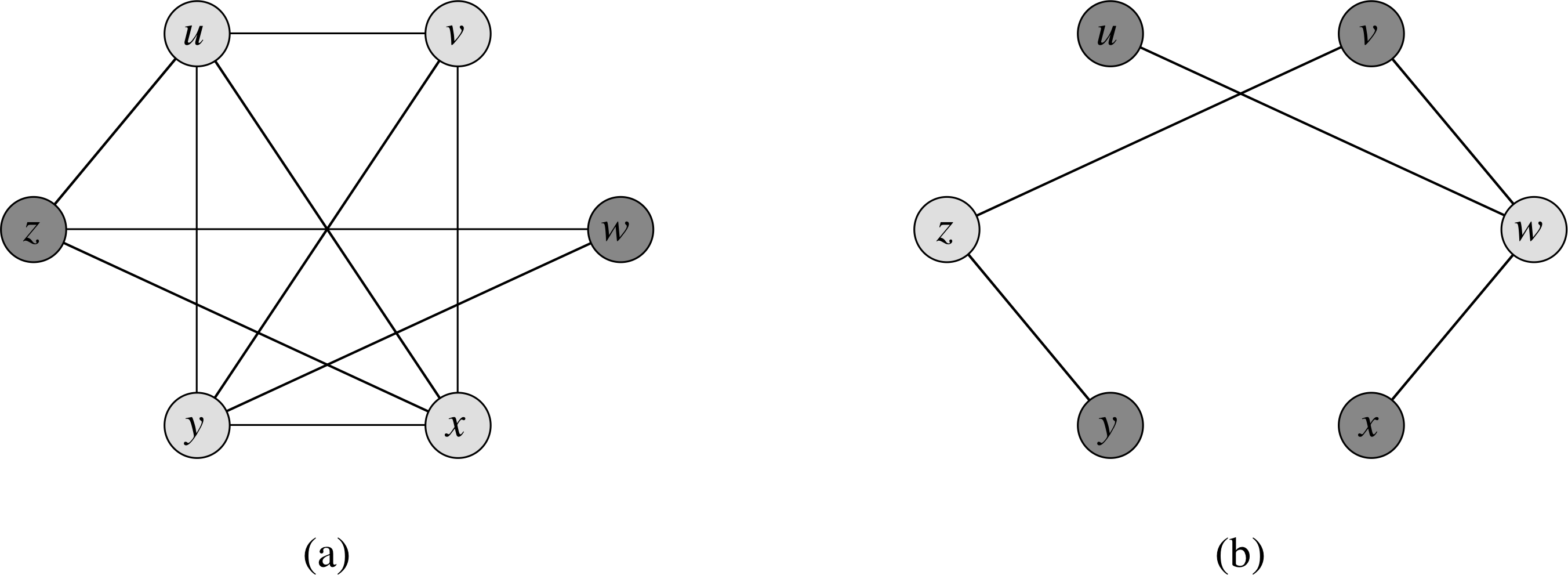
The graph on the left is a graph with a clique of a particular size. In the graph on the left there is a clique of size 4 made up of the light gray vertices. We form the graph on the right by using the same set of vertices but replacing the edges by the complement of the set of edges in the original graph. The new graph will have an edge between two vertices only if the original graph did not have an edge connecting those two vertices.
Suppose that the original graph has a clique of size k. We claim that the set of all vertices not in that clique in the complement graph form a vertex cover of size |V| - k. Consider any edge in the new graph. This edge does not connect two vertices in the clique, since those vertices are all fully connected and edges that connect them would have been removed when we formed the complement. Thus, at least one of the two vertices connected by that edge must be outside the clique, and that vertex can cover that edge. Conversely, suppose the new graph has a vertex cover of size |V| - k. I claim that the set of vertices not in the cover must have formed a clique in the original graph, because the new graph contains no edges connecting those vertices (if it did, that edge would not be covered). When we go backward from the complement graph to the original, all of the vertices not in the cover will have edges restored between them and we will be back to having a clique.
The text shows several additional examples of reductions in section 7.5. The homework assignment for chapter seven includes several problems that ask you to construct your own reductions.