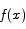is differentiable everywhere in an interval [a,b] and Here is a fundamental theorem about derivatives.
Theorem (Rolle’s Theorem) If 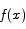is differentiable everywhere in an interval [a,b] and
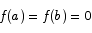
there must exist a point c in [a,b] for which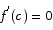 
.
Proof There are two cases. The first case is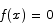 
for all x. In that case we automatically have 
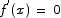for all x, and we are done. If the function is not a constant, we can use the fact that differentiable functions are automatically continuous in combination with the theorem I showed on Monday to claim that f(x) must have at least one max or min between a and b. Max and min points are critical points, so f(x) must have a critical point between a and b. This is what we need: there is a c between a and b for which
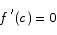
Rolle's theorem is used primarily to prove the following important theorem:
Theorem (Mean Value Theorem) Let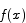 
be a differentiable function on an interval [a,b]. There exists a point c in the interval [a,b] such that
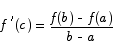
Proof Start by introducing a new function. This function will be the function whose graph is the line connecting the points (a,f(a)) and (b,f(b)). The slope of that line is
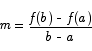
hence the equation of the line is
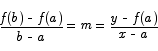
or
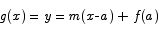
After finding that function, we introduce yet another new function:
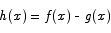
Here are two key properties of h(x):
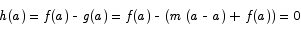
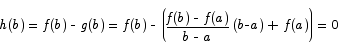
These are the conditions needed to apply Rolle‘s theorem. That theorem then says that there is a c somewhere between a and b for which
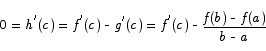
This gets us that
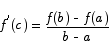
and we are done.
Here is the first in a series of consequences of this theorem.
Theorem If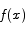 
is differentiable for all x and 
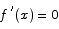for all x, then f(x) must be a constant.
(We already know that if f(x) is a constant,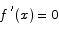 
.)
Proof (by contradiction) Suppose that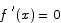 
for all x. By way of contradiction, pretend that f(x) is not a constant function. Since f(x) is not constant, there should exist points a and b for which
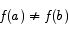
Apply the MVT to points a and b. You get that there is a point c in between a and b for which
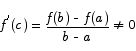
This is a contradiction, so the function must have been constant to start with.
Here is another consequence of the last result.
Corollary If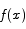 
and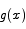 
have the same derivative for all x, f(x) and g(x) differ by a constant.
Proof Introduce a new function h(x) defined by
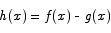
Saying that f(x) and g(x) have the same derivative implies
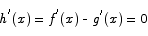
By the previous theorem, h(x) must be a constant.
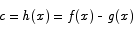
This leads to
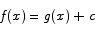
Here is another theorem closely related to the MVT.
Theorem (Cauchy's Form of the MVT) Suppose that the functions f(x) and g(x) are continuous on an interval [a,b ] and differentiable on an interval (a,b) and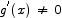 
for all x in (a,b). Then there is a number c in (a,b) such that
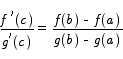
Proof The proof is very similar to the proof of the MVT above. The only difference is in the definition of the function h(x).
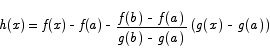
Just as before, h(a) = h(b) = 0, so there is a c between a and b such that
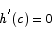
Substituting the definition of h(x) gives
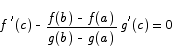
Simple algebra then leads to the result we want.
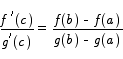
L’Hôpital’s rule is a special technique for computing certain limit problems.
Theorem (L’Hôpital’s rule) If f(x) and g(x) are differentiable functions with the property that
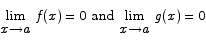
then
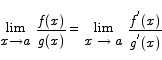
Proof We start by making the assumption that f(a) = g(a) = 0. In the rare cases where this is not true, we have to use a somewhat more clever strategy. (See appendix F for a proof of the stronger result that does not use this assumption.) Since f(a) = g(a) = 0 we can begin by writing
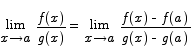
Using Cauchy's form of the MVT we can see that
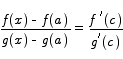
for some c in the interval between x and a. In the limit as x approaches a, c will also approach a.
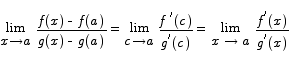
The last equality above results from simply replacing c with x in the limit.
L’Hôpital’s rule is essentially a technique for converting a difficult limit calculation into a simpler calculation. Here are some classic examples.
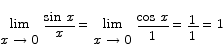
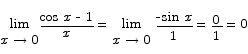
The most common problem with L’Hôpital’s rule is that people who use it forget the requirement that both the numerator and denominator must go to zero in order for the rule to apply. Here is an example of what can happen when the rule is applied inappropriately. The limit
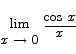
can be evaluated by inspection. The limit is clearly equal to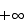 
. If we attempt to apply the rule here we get instead
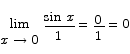
Sometimes one has to apply the rule more than once to resolve a limit question.
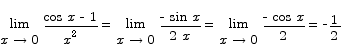
Here is a second form for L’Hôpital’s rule that I present without proof. (If you are curious, the proof is available in Appendix F.)
Theorem (L’Hôpital’s rule,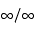 
case) Let f(x) and g(x) be functions for which
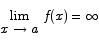
and
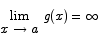
Then
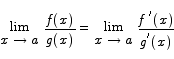
This is useful for the following example
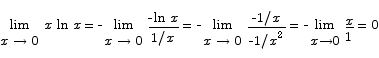
Section 4.2: 5, 26, 32
Section 4.4: 5, 6, 15, 16, 22, 23, 37, 38