numpy vector functions
Here is an example that I showed in the first lecture this term.
import matplotlib.pyplot as plt import numpy as np t = np.arange(-np.pi, np.pi, 0.01) s = np.sin(t) plt.plot(t, s) plt.show()
This example uses a combination of numpy and pyplot to construct a plot of the curve y = sin x. As you know from our previous discussion of pyplot, the plot() method expects two parameters. The first is a list of x coordinates for a set of points to plot, while the second is a list of y coordinates for those points. It turns out that plot() will accept other things besides plain lists. plot() will also accept as its parameters any objects that are iterable.
The parameters we are preparing and passing to plot() in this example are both numpy array objects. To construct the array t we make use of the numpy arange() method. arange() takes three parameters, a starting point, an ending point, and a step size, and returns an array object for a row vector. The row vector contains a list of all of the sample points in the requested range. In this example the list of sample points consists of something more than 600 points spaced 0.01 units apart.
The line
s = np.sin(t)
then implements what numpy calls a vector operation. This operation applies the function sin x to each of the x values in the vector t, resulting in a new vector s that contains the y values we need for our plot.
numpy contains a large number of such vector functions. Each of these functions will take a vector as their parameter and return a new vector whose entries are the result of applying the function to each of the original entries in turn. In addition to these vector functions, numpy also overloads just about every arithmetic operator to implement vector arithmetic operations.
Here is a slightly fancier version of the last example. In this version we will use the numpy vector functions to instead make a plot of y = 3 sin (x - 2):
import matplotlib.pyplot as plt import numpy as np t = np.arange(-np.pi, np.pi, 0.01) s = 3*np.sin(t-2) plt.plot(t, s) plt.show()
The arithmetic operators in this example apply a scalar transformation to each entry in a numpy array. For example, t-2 produces a new array each of whose entries is an entry from t with the scalar 2 subtracted from it.
aggregation functions
numpy vector operations really come into their own when used in combination with aggregation functions. The simplest and most powerful aggregation function is sum(), which returns the sum of all of the entries in a vector.
Here is an earlier example rewritten to take advantage of numpy vector operations. The example is the Romberg integration example I showed earlier in the term. The first step in Romberg integration is to compute a trapezoid rule estimate via the formula
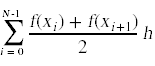
Another way to write this formula is to note that with the exception of the first and last terms in the summation every sample point appears twice here. This allows us to rewrite this sum as

To compute the sum in the center of this expression we start by making a numpy array that represents all of the sample points between a and b. We then pass that array through the vector function f(x)*h, and then apply the sum() operation to add up all of those terms.
Here now is the code for the complete example, with the logic to compute the trapezoid rule replaced with numpy vector evaluation code.
import numpy as np
# This is the function we will work with for this example
def f(x):
return np.sqrt(4.0 - (2.0-x)*(2.0-x))
# Compute an approximation to the integral
# of f(x) from a to b by using trapezoids
# with steps of size (b-a)/N
def trapezoidArea(a,b,N):
h = (b - a)/N;
x = np.arange(a,b,h)
return h*(f(x).sum()) - h*f(a)/2 - h*f(b)/2
# Recursively defined Romberg formula with caching
# r_int will compute R[k,j] but then remember that
# result in the R list to speed up subsequent calculations.
def r_int(a,b,k,j,R):
if R[k][j] != -1: # Have we seen this k,j before?
return R[k][j] # If so, just return the cached value
# If not, compute, cache, and return the result
if j == 1:
R[k][j] = trapezoidArea(a,b,2**(k-1))
elif k < j:
R[k][j] = 0
else:
R[k][j] = r_int(a,b,k,j-1,R) + (r_int(a,b,k,j-1,R)-r_int(a,b,k-1,j-1,R))/(4**(j-1)-1)
return R[k][j]
def romberg(a,b,k,j):
R = [[-1 for c in range(j+1)] for r in range(k+1)]
return r_int(a,b,k,j,R)
print(" j estimate error");
for j in range(3,22,2):
estimate = romberg(0.0,2.0,j,j)
error = np.fabs(np.pi - estimate)
print("{:>3d} {:f} {:.16f}".format(j,estimate,error))
numpy vector code is fast
Beyond allowing us to apply some slick optimizations to things like the trapezoid rule, there is a further compelling reason to use numpy vector operations. These operations are highly optimized to run as fast as possible in practice. One peculiar trick that vector code takes advantage of is parallelization. On machines that have multiple processing cores (which is most machines these days), numpy will take a vector operation and break it into chunks, running each chunk of the computation on a separate processor core. For example, on a four core machine numpy will split each vector it processes into four equal sized subvectors and then perform the computations for those separate parts on four separate cores. The net effect is a speed-up of about a factor of four on every vector operation we do.
You can immediately see this by running both the ordinary version of the Romberg program and the numpy version. The numpy version is noticeably faster.